4 Is What Percent Of 9
Treneri
May 11, 2025 · 4 min read
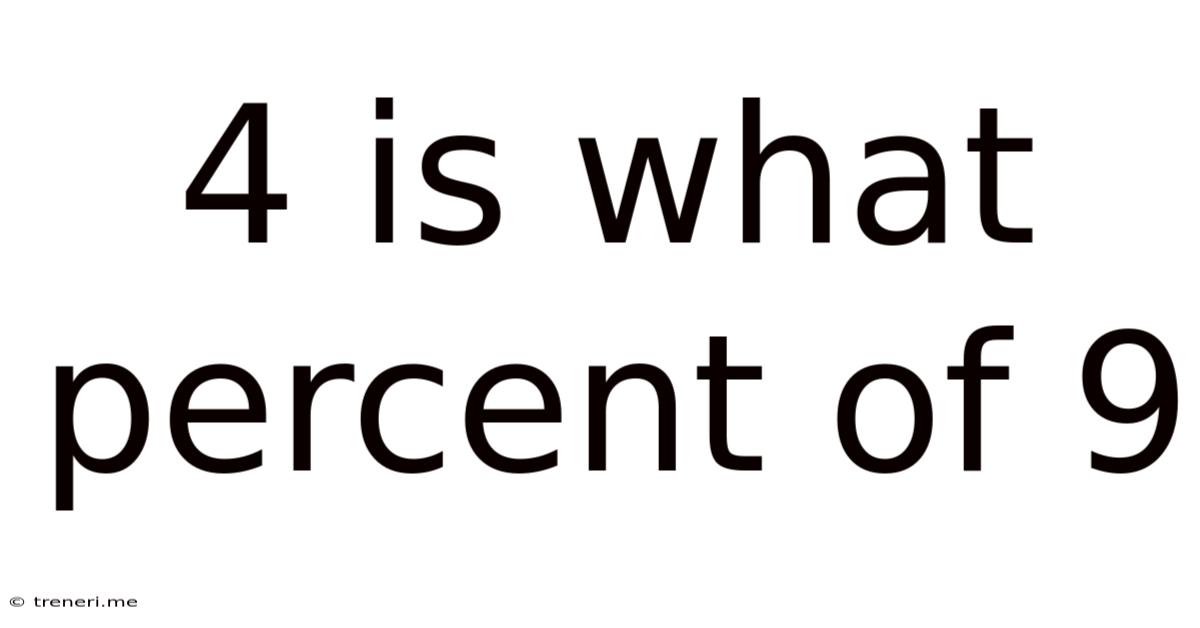
Table of Contents
4 is What Percent of 9? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with wide-ranging applications in daily life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves into the question, "4 is what percent of 9?", providing a step-by-step solution, exploring different approaches, and expanding on the broader concept of percentage calculations. We'll also touch on practical applications and common mistakes to avoid.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." For instance, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Calculating "4 is What Percent of 9?"
To determine what percentage 4 represents of 9, we need to follow these steps:
Step 1: Set up the Equation
We can represent the problem as an equation:
x/100 = 4/9
Where 'x' represents the percentage we are trying to find.
Step 2: Solve for x
To solve for 'x', we can cross-multiply:
9x = 4 * 100
9x = 400
Now, divide both sides by 9:
x = 400/9
x ≈ 44.44
Step 3: State the Answer
Therefore, 4 is approximately 44.44% of 9.
Alternative Methods
While the above method is straightforward, there are other ways to approach this problem:
Method 1: Using Decimal Conversion
-
Divide 4 by 9: This gives us the decimal equivalent of the fraction 4/9: 4 ÷ 9 ≈ 0.4444
-
Convert the decimal to a percentage: Multiply the decimal by 100: 0.4444 * 100 ≈ 44.44%
Method 2: Using Proportions
We can set up a proportion:
4/9 = x/100
Cross-multiplying and solving for 'x' will yield the same result as the first method.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in various real-world scenarios:
-
Financial Calculations: Calculating discounts, interest rates, taxes, tips, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding sales tax percentages allows you to accurately predict the final cost of a purchase. Similarly, grasping interest rates is vital for managing loans and investments.
-
Data Analysis: Percentages are essential for interpreting statistical data, comparing proportions, and visualizing trends. For instance, analyzing market share data often involves expressing market segments as percentages of the total market.
-
Scientific Calculations: Percentages play a role in many scientific fields, such as calculating concentrations in chemistry, analyzing experimental results, and representing changes in populations in biology.
-
Everyday Life: Percentages are used in many everyday situations, such as calculating the percentage of a task completed, figuring out nutritional information, or understanding survey results.
Common Mistakes to Avoid
Several common mistakes can lead to inaccurate percentage calculations:
-
Confusing the numerator and denominator: Ensure you correctly identify which number represents the part (numerator) and which represents the whole (denominator). In our example, 4 is the part, and 9 is the whole.
-
Incorrect decimal-to-percentage conversion: Remember to multiply the decimal by 100 to convert it to a percentage. Failing to do so will lead to an answer that is off by a factor of 100.
-
Rounding errors: While rounding is sometimes necessary, be mindful of potential inaccuracies introduced by rounding intermediate results. It's generally best to round only the final answer.
-
Using the wrong formula: Ensure you use the appropriate formula for the specific percentage calculation you're performing. There are different formulas for calculating percentage increase, percentage decrease, percentage change, and so on.
Expanding on Percentage Concepts
Understanding percentages opens doors to a wide range of mathematical concepts:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] * 100. The formula for percentage decrease is analogous. -
Percentage Points: This is often confused with percentage change. A percentage point refers to an absolute change in percentage values. For example, if the interest rate increases from 5% to 8%, this is a 3-percentage point increase, not a 60% increase.
-
Compounding Percentages: This involves applying a percentage change repeatedly over time, as seen in compound interest calculations. This is a more complex concept but crucial for long-term financial planning.
Conclusion: Mastering Percentage Calculations
Calculating percentages is a versatile skill applicable to diverse fields. By understanding the basic principles, utilizing different calculation methods, and avoiding common pitfalls, you can confidently tackle percentage problems and utilize this valuable tool in your daily life and professional endeavors. Remember, practice makes perfect. Try working through various percentage problems to solidify your understanding and build confidence in your ability to accurately perform these calculations. The seemingly simple question, "4 is what percent of 9?", serves as a gateway to understanding a much broader and more important concept in mathematics and its applications.
Latest Posts
Latest Posts
-
Calcular Los Interes De Un Carro
May 12, 2025
-
What Is 60 100 As A Grade
May 12, 2025
-
Cuantas Horas Faltan Para El Lunes
May 12, 2025
-
5 4 5 As An Improper Fraction
May 12, 2025
-
What Is The Area Of The Rhombus Shown Below
May 12, 2025
Related Post
Thank you for visiting our website which covers about 4 Is What Percent Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.