4 Out Of 13 As A Percentage
Treneri
May 13, 2025 · 5 min read
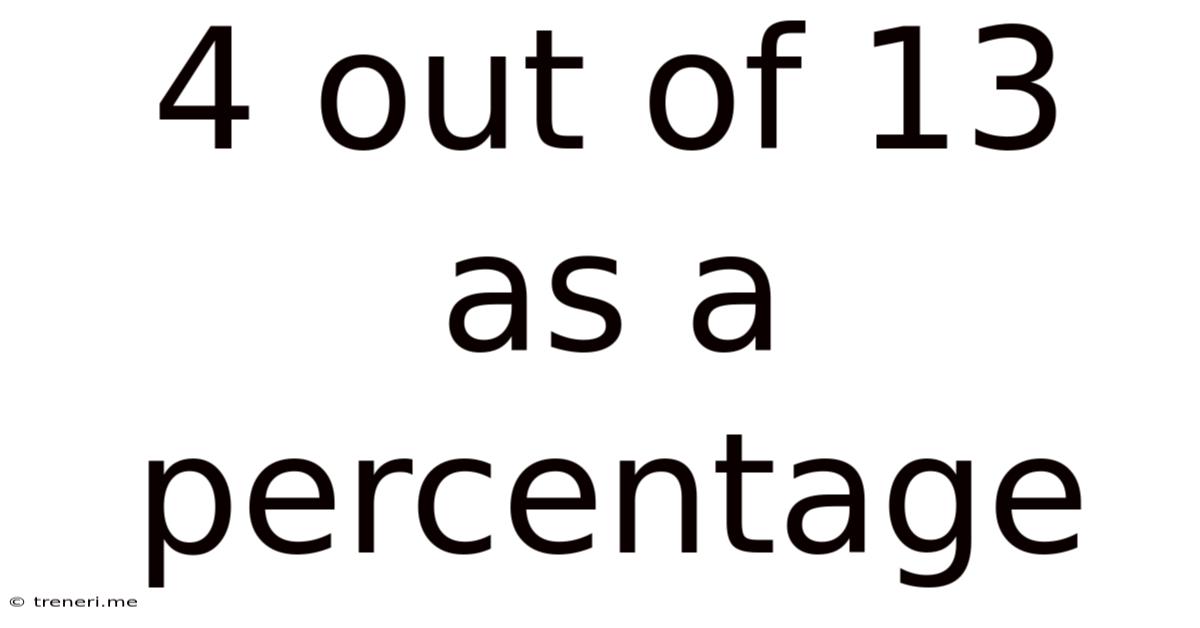
Table of Contents
4 Out of 13 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with applications spanning numerous fields, from everyday finances to complex statistical analyses. Understanding how to convert fractions into percentages is crucial for accurate interpretations and informed decision-making. This comprehensive guide will delve into the process of calculating "4 out of 13 as a percentage," exploring various methods, providing step-by-step instructions, and offering valuable insights into percentage calculations in general.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The term "percent" itself originates from the Latin "per centum," meaning "out of a hundred." Therefore, 25% means 25 out of 100, which can also be expressed as the fraction 25/100 or the decimal 0.25.
Method 1: Using the Fraction Method
The most straightforward approach to calculating "4 out of 13 as a percentage" involves converting the given ratio into a fraction and then expressing that fraction as a percentage.
Step 1: Express as a Fraction
The phrase "4 out of 13" translates directly into the fraction 4/13.
Step 2: Convert the Fraction to a Decimal
To convert the fraction 4/13 into a decimal, we perform the division: 4 ÷ 13 ≈ 0.3077
Step 3: Convert the Decimal to a Percentage
To express the decimal as a percentage, we multiply by 100: 0.3077 x 100 = 30.77%
Therefore, 4 out of 13 is approximately 30.77%.
Method 2: Using Proportions
Another method utilizes proportions to solve this problem. This method is particularly useful when dealing with more complex percentage calculations.
Step 1: Set up a Proportion
We set up a proportion where x represents the percentage we want to find:
4/13 = x/100
Step 2: Cross-Multiply
To solve for x, we cross-multiply:
13x = 400
Step 3: Solve for x
Divide both sides by 13:
x = 400/13 ≈ 30.77
Step 4: Express as a Percentage
Therefore, x ≈ 30.77%, confirming our previous result.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations significantly. Most calculators have a percentage function (%) that directly performs the conversion.
Step 1: Input the Fraction
Enter the fraction 4/13 into your calculator.
Step 2: Use the Percentage Function
Press the percentage function button (%). The calculator will display the result as a percentage.
Step 3: Interpret the Result
The calculator should display approximately 30.77%, providing a quick and efficient solution.
Rounding Percentages
The result of 30.77% is an approximation. Depending on the context, rounding might be necessary. Common rounding practices include:
- Rounding to the nearest whole number: 31%
- Rounding to one decimal place: 30.8%
- Rounding to two decimal places: 30.77%
The appropriate level of rounding depends on the required precision for your application. For instance, in informal settings, rounding to the nearest whole number might suffice, while scientific or financial contexts often demand greater accuracy.
Applications of Percentage Calculations
Understanding percentage calculations is essential in a wide range of applications, including:
- Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns.
- Statistics: Analyzing data, interpreting survey results, and understanding probability.
- Science: Expressing experimental results, calculating concentrations, and representing data graphically.
- Everyday Life: Calculating tips, understanding sale prices, and comparing different options.
Advanced Percentage Calculations: Understanding Percentage Increase/Decrease
Beyond basic percentage calculations, understanding percentage increases and decreases is crucial. Suppose, for instance, a product's price increased from $10 to $13. To calculate the percentage increase:
Step 1: Find the difference: $13 - $10 = $3
Step 2: Divide the difference by the original value: $3 / $10 = 0.3
Step 3: Multiply by 100 to express as a percentage: 0.3 x 100 = 30%
Therefore, the price increased by 30%.
Similarly, percentage decreases are calculated by following the same steps, using the original value as the denominator.
Percentage Points vs. Percentage Change
It's important to differentiate between "percentage points" and "percentage change." A percentage point refers to an absolute change in percentage values, while percentage change represents a relative change. For example:
If interest rates rise from 5% to 8%, the increase is 3 percentage points. However, the percentage change is calculated as (8-5)/5 * 100 = 60%.
Practical Examples of 4 out of 13
Let's illustrate the practical application of understanding "4 out of 13" as approximately 30.77% with a few real-world scenarios:
- Test Scores: If a student answered 4 out of 13 questions correctly on a quiz, their score is approximately 30.77%.
- Survey Results: If 4 out of 13 respondents to a survey prefer a particular product, this represents approximately 30.77% of the respondents.
- Inventory Management: If 4 out of 13 items in a shipment are damaged, approximately 30.77% of the shipment is damaged.
- Production Quality Control: If 4 out of 13 manufactured items fail quality checks, the failure rate is approximately 30.77%.
Conclusion
Calculating percentages is a valuable skill applicable across diverse fields. Understanding the various methods, including the fraction method, proportion method, and calculator methods, allows for flexibility and efficient calculation. Remember to consider the context and round appropriately for clarity. Mastering percentage calculations empowers you to interpret data accurately, make informed decisions, and solve problems effectively in both professional and personal settings. By understanding concepts such as percentage increase/decrease and the difference between percentage points and percentage change, you can enhance your analytical capabilities and communicate quantitative information with greater precision. The seemingly simple calculation of "4 out of 13 as a percentage" serves as a gateway to understanding a fundamental concept with far-reaching implications.
Latest Posts
Latest Posts
-
How Many Hours Is 127 Minutes
May 14, 2025
-
Write The Number 0 0005 In Scientific Notation
May 14, 2025
-
Greatest Common Factor Of 34 And 51
May 14, 2025
-
What Is 16 Rounded To The Nearest 10
May 14, 2025
-
How Many More Fridays Until Fall
May 14, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 13 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.