4 Times 10 To The Power Of 3
Treneri
May 10, 2025 · 5 min read
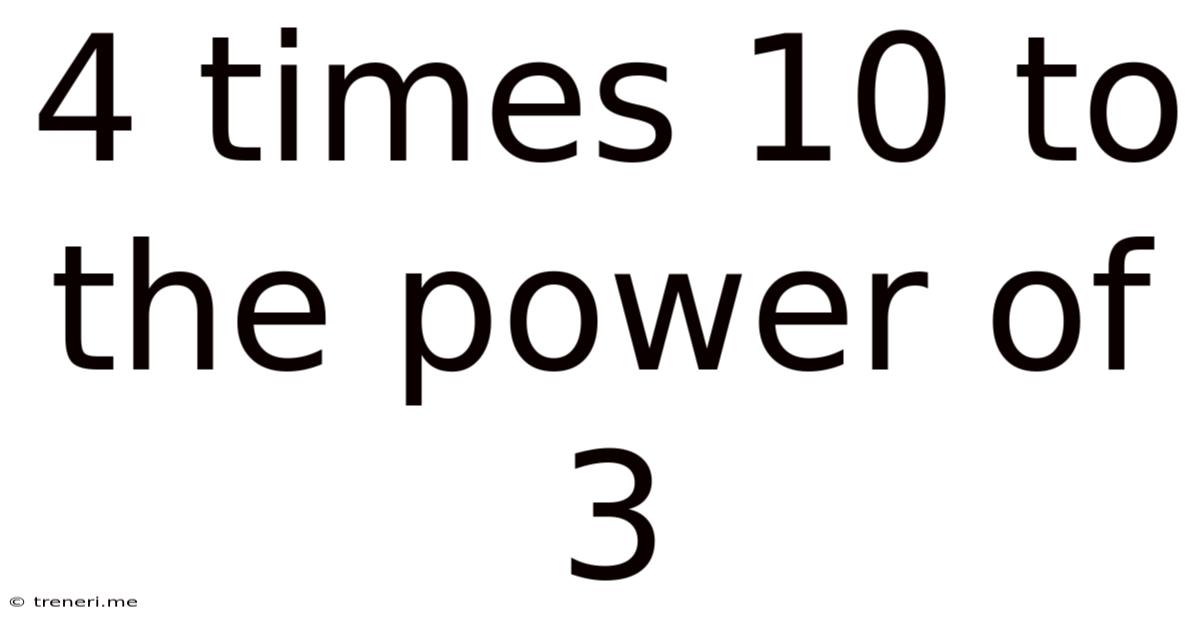
Table of Contents
4 Times 10 to the Power of 3: Unpacking Scientific Notation and its Applications
Scientific notation, a cornerstone of scientific and engineering disciplines, provides a concise way to represent extremely large or small numbers. Understanding this notation is crucial for comprehending various scientific concepts and performing calculations involving vast or minuscule quantities. This article delves deep into the meaning and implications of "4 times 10 to the power of 3," exploring its mathematical representation, practical applications across different fields, and its significance in scientific communication.
Understanding Scientific Notation
Scientific notation expresses numbers in the form a × 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer exponent. This format simplifies the handling of very large or very small numbers that would otherwise be cumbersome to write and work with. For example, the number 3,000,000,000 can be expressed in scientific notation as 3 × 10<sup>9</sup>. Similarly, a tiny number like 0.000000003 can be written as 3 × 10<sup>-9</sup>.
The exponent 'b' indicates the number of places the decimal point needs to be moved to obtain the original number. A positive exponent signifies a large number, meaning the decimal point is shifted to the right. A negative exponent indicates a small number, requiring the decimal point to be shifted to the left.
Decoding 4 x 10³
Let's focus on the specific expression: 4 times 10 to the power of 3 (4 × 10³). This represents the number 4 multiplied by 10 raised to the power of 3. Since 10³ (10 to the power of 3) equals 10 × 10 × 10 = 1000, the expression simplifies to 4 × 1000.
Therefore, 4 × 10³ = 4000. This relatively straightforward example demonstrates the simplicity and efficiency of scientific notation. Imagine trying to perform calculations with extremely large numbers like Avogadro's number (approximately 6.022 × 10²³) without this system – it would be incredibly tedious and prone to errors.
Applications of Scientific Notation and 4 x 10³
The application of scientific notation, and numbers like 4 × 10³, pervades various scientific and engineering domains. Here are some examples:
1. Measurement and Units:
- Volume: Imagine measuring the volume of a large container in cubic meters. If the volume is 4000 cubic meters, it is much simpler and clearer to express this as 4 × 10³ m³. This notation is universally understood and avoids ambiguity.
- Mass: In physics, dealing with mass often involves large numbers. For instance, a mass of 4000 kilograms could be easily represented as 4 × 10³ kg.
- Distance: Similarly, expressing vast distances in astronomy, such as 4000 kilometers, becomes manageable using scientific notation: 4 × 10³ km.
2. Data Representation in Computer Science:
- Memory: Computers store information in units of bytes, kilobytes, megabytes, and so on. A computer with 4000 kilobytes of RAM can be described as having 4 × 10³ KB of RAM. Understanding this notation is crucial for managing computer resources.
- Data Transfer: In networking, data transfer rates are often expressed using scientific notation. A transfer rate of 4000 bits per second would be 4 × 10³ bps.
3. Physics and Engineering:
- Force and Energy: Calculations in physics involving force and energy frequently use scientific notation because the numbers can get very large (e.g., calculating the energy released in a nuclear reaction).
- Wave Phenomena: The frequency of electromagnetic waves, like radio waves or light waves, often involves large numbers best expressed using scientific notation.
- Electrical Engineering: Electrical currents and voltages can also necessitate the use of scientific notation, particularly when dealing with high-power systems.
4. Chemistry:
- Mole Calculations: In chemistry, the concept of a mole (Avogadro's number) is essential for stoichiometric calculations. Representing the number of molecules or atoms often involves numbers of the magnitude of 4 × 10³ or even much larger.
- Concentration: Concentrations of solutions are frequently expressed using scientific notation, especially when dealing with dilute solutions.
5. Biology:
- Microbial Populations: Counting microorganisms in a sample often leads to very large numbers, readily handled with scientific notation.
- Genetic Sequences: The length of DNA sequences in genetics can be very long and are best represented in scientific notation.
6. Finance:
- Large Investments: In finance, dealing with large sums of money often involves scientific notation, particularly when dealing with national budgets or global investment portfolios. While 4 × 10³ might represent a smaller scale investment, the principle remains the same for much larger amounts.
Beyond the Basics: Working with Scientific Notation
Understanding 4 × 10³ is just the first step. To fully grasp scientific notation, it's crucial to know how to perform calculations with it. This involves:
- Multiplication: When multiplying numbers in scientific notation, multiply the 'a' values and add the 'b' values. For example: (2 × 10²) × (2 × 10³) = 4 × 10⁵.
- Division: When dividing numbers in scientific notation, divide the 'a' values and subtract the 'b' values. For example: (6 × 10⁵) / (3 × 10²) = 2 × 10³.
- Addition and Subtraction: Before adding or subtracting numbers in scientific notation, the exponents must be the same. This might require adjusting the 'a' value and the exponent accordingly.
The Importance of Scientific Notation in Communication
Beyond its mathematical utility, scientific notation plays a vital role in clear and concise scientific communication. It helps to:
- Avoid ambiguity: Scientific notation eliminates the potential for misinterpreting large or small numbers due to misplaced decimal points or missing zeros.
- Improve readability: It makes scientific papers, reports, and presentations easier to read and understand.
- Enhance accuracy: It minimizes errors that can occur when working with very large or small numbers manually.
- Facilitate global understanding: Its standardized format ensures universal comprehension across different languages and regions.
Conclusion: The Significance of 4 x 10³ and Beyond
While 4 × 10³ might seem like a simple expression, it encapsulates the power and efficiency of scientific notation. This notation is not just a mathematical tool; it's a fundamental component of scientific literacy and clear communication across various disciplines. Understanding this concept and the principles behind scientific notation lays the foundation for comprehending complex scientific ideas and tackling real-world problems involving vast or minute quantities. The ability to confidently manipulate and interpret numbers in scientific notation is a critical skill for students and professionals alike in a wide range of fields. Mastering this skill unlocks a deeper understanding of the numerical world around us, from the smallest subatomic particles to the largest celestial bodies.
Latest Posts
Latest Posts
-
Round 66 To The Nearest Ten
May 10, 2025
-
Cuanto Falta Para El 18 De Noviembre
May 10, 2025
-
If A Triangle Has A Height Of 12 Inches
May 10, 2025
-
Cuanto Es 90 Cm En Pies
May 10, 2025
-
50 Miles Per Gallon To Kmpl
May 10, 2025
Related Post
Thank you for visiting our website which covers about 4 Times 10 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.