41 Is 82 Of What Number
Treneri
May 12, 2025 · 5 min read
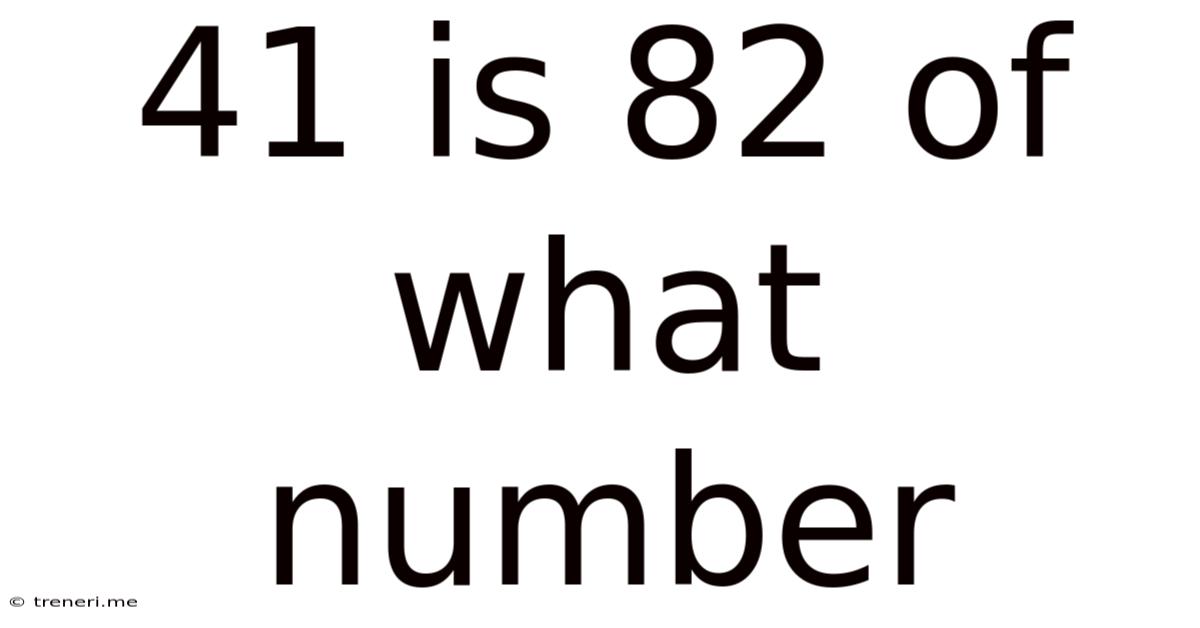
Table of Contents
41 is 82% of What Number? A Deep Dive into Percentage Calculations
Finding the answer to "41 is 82% of what number?" might seem like a simple math problem, but understanding the underlying concepts unlocks a world of practical applications in various fields. This article will not only provide the solution but also explore the different methods for solving percentage problems, explaining the reasoning behind each step. We'll delve into the practical implications of percentage calculations and provide you with the tools to tackle similar problems confidently.
Understanding Percentages: The Foundation
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred." So, 82% means 82 out of 100, or 82/100, which simplifies to 41/50 as a fraction.
This fundamental understanding is key to solving percentage problems effectively. We use percentages to express proportions, rates, and changes across various disciplines, from finance and statistics to everyday life.
Method 1: Using the Percentage Formula
The most direct approach to solving "41 is 82% of what number?" involves using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part: 41 (the given amount)
- Percentage: 82% (expressed as a decimal: 0.82)
- Whole: This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
41 = 0.82 × x
To solve for 'x', we divide both sides of the equation by 0.82:
x = 41 / 0.82
x = 50
Therefore, 41 is 82% of 50.
Method 2: Using Proportions
Another effective method for solving percentage problems involves setting up a proportion. A proportion shows the equality of two ratios. We can represent the problem as:
41/x = 82/100
This proportion states that the ratio of 41 to the unknown number (x) is equal to the ratio of 82 to 100 (which represents 82%).
To solve for x, we can cross-multiply:
41 × 100 = 82 × x
4100 = 82x
Now, divide both sides by 82:
x = 4100 / 82
x = 50
Again, we find that 41 is 82% of 50.
Method 3: Working Backwards from the Percentage
We can also approach this problem by considering what 1% represents. If 82% is equal to 41, then we can find the value of 1% by dividing 41 by 82:
1% = 41 / 82 = 0.5
Since 1% is equal to 0.5, we can find the whole (100%) by multiplying 0.5 by 100:
100% = 0.5 × 100 = 50
This confirms that 41 is 82% of 50.
Practical Applications of Percentage Calculations
The ability to solve percentage problems extends far beyond simple mathematical exercises. Understanding percentages is crucial in various real-world scenarios:
1. Finance and Investing:
- Calculating returns on investments: Determining the percentage increase or decrease in the value of investments over time.
- Understanding interest rates: Calculating simple and compound interest on loans and savings accounts.
- Analyzing financial statements: Interpreting profit margins, revenue growth, and other key financial metrics expressed as percentages.
- Discount calculations: Determining the final price of an item after a percentage discount is applied.
2. Sales and Marketing:
- Tracking sales performance: Measuring sales growth, conversion rates, and customer acquisition costs as percentages.
- Analyzing market share: Determining a company's percentage of the total market for a particular product or service.
- Setting pricing strategies: Calculating markup percentages to determine selling prices.
- Evaluating marketing campaign effectiveness: Measuring the percentage of leads generated, website traffic, and sales attributed to specific marketing campaigns.
3. Everyday Life:
- Calculating tips and gratuities: Determining the appropriate tip percentage in restaurants and other service industries.
- Understanding sales taxes: Calculating the total cost of an item including sales tax.
- Comparing prices: Determining the best value for money by comparing prices and percentages.
- Analyzing survey results: Interpreting survey data expressed as percentages to understand consumer preferences and opinions.
4. Science and Statistics:
- Expressing probability: Representing the likelihood of an event occurring as a percentage.
- Analyzing experimental data: Calculating percentage changes, error rates, and other statistical measures.
- Representing population demographics: Showing the percentage of a population with certain characteristics (age, gender, etc.).
Expanding Your Percentage Skills: Beyond the Basics
While the problem "41 is 82% of what number?" serves as a great introduction to percentage calculations, mastering percentages involves tackling more complex scenarios. Here are some areas to explore to further enhance your skills:
- Percentage increase and decrease: Learn to calculate the percentage change between two values.
- Compound percentages: Understand how percentages can accumulate over time, such as with compound interest.
- Percentage points vs. percentage change: Distinguish between these two concepts to avoid confusion.
- Solving for the percentage: Practice problems where you need to find the percentage when the part and whole are given.
- Applying percentages to real-world problems: Seek opportunities to apply your knowledge of percentages to solve problems in your daily life, work, or studies.
Conclusion: Mastering Percentages for a Brighter Future
The ability to confidently solve percentage problems like "41 is 82% of what number?" is a valuable skill applicable across numerous domains. By understanding the underlying principles, utilizing various calculation methods, and practicing consistently, you will not only improve your mathematical proficiency but also gain a valuable tool for navigating the complexities of the real world. Remember that consistent practice and application are key to mastering percentages and utilizing them effectively in your daily life and professional endeavors. The more you practice, the more intuitive these calculations will become, allowing you to efficiently solve percentage problems in various contexts.
Latest Posts
Latest Posts
-
Find The Indicated Side Of The Triangle
May 12, 2025
-
Tiempo De Embarazo De Las Gatas
May 12, 2025
-
90 Days From July 5th 2024
May 12, 2025
-
How Many Miles Is 1024 Kilometers
May 12, 2025
-
180 Rounded To The Nearest Tenth
May 12, 2025
Related Post
Thank you for visiting our website which covers about 41 Is 82 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.