46.5 Out Of 50 As A Percentage
Treneri
May 12, 2025 · 4 min read
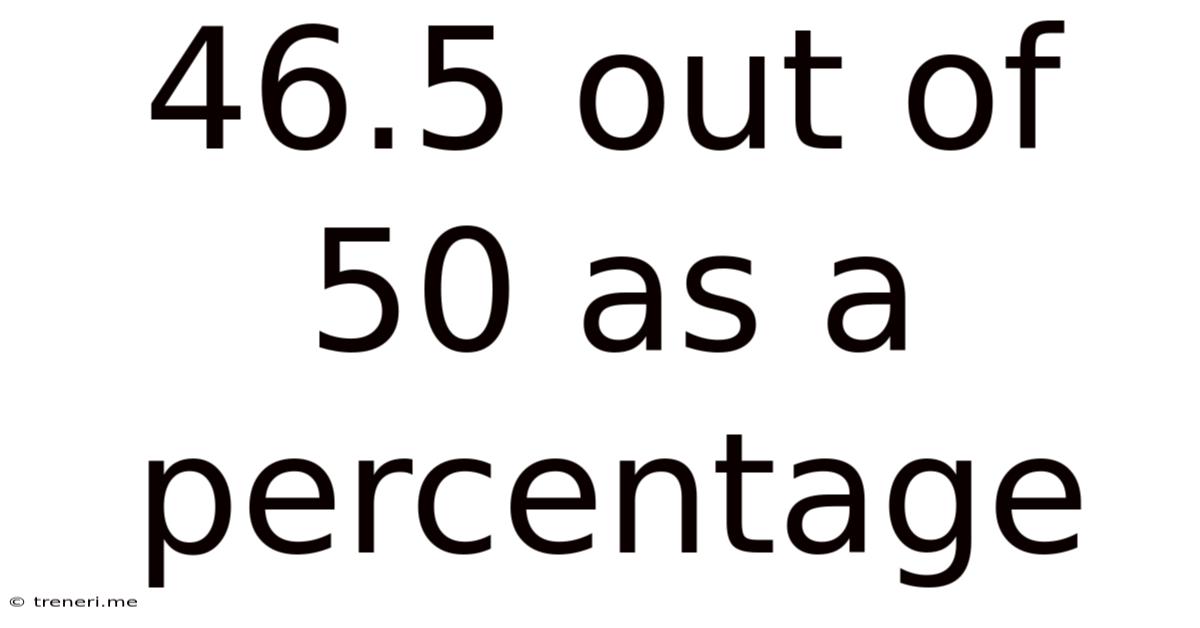
Table of Contents
Decoding 46.5 out of 50 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. Understanding how to convert fractions and decimals into percentages is crucial for interpreting data and making informed decisions. This article dives deep into the calculation and implications of 46.5 out of 50, exploring various methods and providing practical examples.
Understanding the Fundamentals of Percentages
Before we tackle the specific calculation of 46.5 out of 50, let's revisit the basic principles of percentages. A percentage represents a fraction of 100. The term "percent" literally means "out of 100." Therefore, to express any fraction or decimal as a percentage, we need to find its equivalent value out of 100.
The Formula:
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Where:
- Part: Represents the specific portion we're interested in.
- Whole: Represents the total amount or the complete quantity.
Calculating 46.5 out of 50 as a Percentage
Now, let's apply this formula to our specific problem: 46.5 out of 50.
In this scenario:
- Part = 46.5
- Whole = 50
Substituting these values into the formula:
(46.5 / 50) * 100 = Percentage
1. Division:
First, we divide the part (46.5) by the whole (50):
46.5 / 50 = 0.93
2. Multiplication:
Next, we multiply the result by 100 to express it as a percentage:
0.93 * 100 = 93
Therefore, 46.5 out of 50 is equal to 93%.
Different Approaches to the Calculation
While the above method is the most straightforward, let's explore alternative methods to arrive at the same conclusion. These alternative approaches can be useful depending on the context and the tools available.
Method 2: Using Proportions:
We can solve this problem using proportions. We can set up a proportion where x represents the percentage:
46.5/50 = x/100
Cross-multiplying, we get:
50x = 4650
Dividing both sides by 50:
x = 93
Therefore, x = 93%, confirming our previous calculation.
Method 3: Mental Math Techniques (Approximation)
For quick estimations, we can use mental math techniques. We know that 50 is half of 100. Therefore, if we had 25 out of 50, that would be 50%. Since 46.5 is almost double 25, we can reasonably estimate the percentage to be close to 90%. This provides a useful approximation before performing the precise calculation.
Interpreting the Result: 93%
A score of 93% represents a very high achievement. This signifies that the individual or entity in question performed exceptionally well, achieving almost the entirety of the available points or targets. The interpretation of this percentage will heavily depend on the context:
-
Academic Context: In an academic setting, a 93% would typically be considered an A or A+ grade, indicating mastery of the subject matter.
-
Business Context: In a business context, a 93% success rate for a project or campaign would indicate a very successful outcome, possibly exceeding expectations.
-
Statistical Context: In statistical analysis, a 93% confidence interval implies a high degree of certainty in the result.
Practical Applications of Percentage Calculations
Understanding percentage calculations extends far beyond simple academic exercises. It's a crucial skill in various real-world scenarios:
-
Financial Planning: Calculating interest rates, investment returns, and loan repayments all rely on percentage calculations.
-
Sales and Marketing: Analyzing sales figures, conversion rates, and customer satisfaction scores requires understanding percentages.
-
Data Analysis: Interpreting statistical data, creating charts and graphs, and drawing conclusions frequently involves percentage calculations.
-
Everyday Life: Calculating discounts, tips, and taxes are everyday examples where understanding percentages is invaluable.
Common Percentage Calculation Mistakes to Avoid
While percentage calculations seem straightforward, several common errors can lead to inaccurate results. Here are some mistakes to watch out for:
-
Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Decimal Point Errors: Pay close attention to the placement of decimal points, especially when working with decimals and percentages.
-
Mixing Up Part and Whole: Clearly identify the part and the whole before applying the formula. Confusing these two can lead to incorrect results.
-
Calculation Errors: Double-check your calculations to avoid simple arithmetic errors. Use a calculator when necessary to ensure accuracy.
Advanced Applications and Further Exploration
The principles discussed above form the foundation for more complex percentage calculations. These include:
-
Percentage Change: Calculating the percentage increase or decrease between two values.
-
Percentage Points: Understanding the difference between percentage change and percentage points.
-
Compound Interest: Calculating interest that is earned not only on the principal but also on accumulated interest.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable life skill. This article has provided a comprehensive guide to calculating 46.5 out of 50 as a percentage, exploring various methods, and highlighting the importance of accuracy in these calculations. By understanding the underlying principles and avoiding common errors, you can confidently apply these skills in various contexts, from academic assessments to professional endeavors. Remember that practicing regularly is key to building proficiency and ensuring accuracy in your percentage calculations. The more you practice, the more comfortable and confident you will become in tackling these essential mathematical concepts.
Latest Posts
Latest Posts
-
What Is An Equivalent Fraction For 4 10
May 15, 2025
-
What Is A 21 30 In Percentage
May 15, 2025
-
What Grade Is A 9 Out Of 14
May 15, 2025
-
Cuanto Es 16 Onzas En Mililitros
May 15, 2025
-
What Is 175 Cm In Height
May 15, 2025
Related Post
Thank you for visiting our website which covers about 46.5 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.