47 6 As A Mixed Number
Treneri
May 15, 2025 · 5 min read
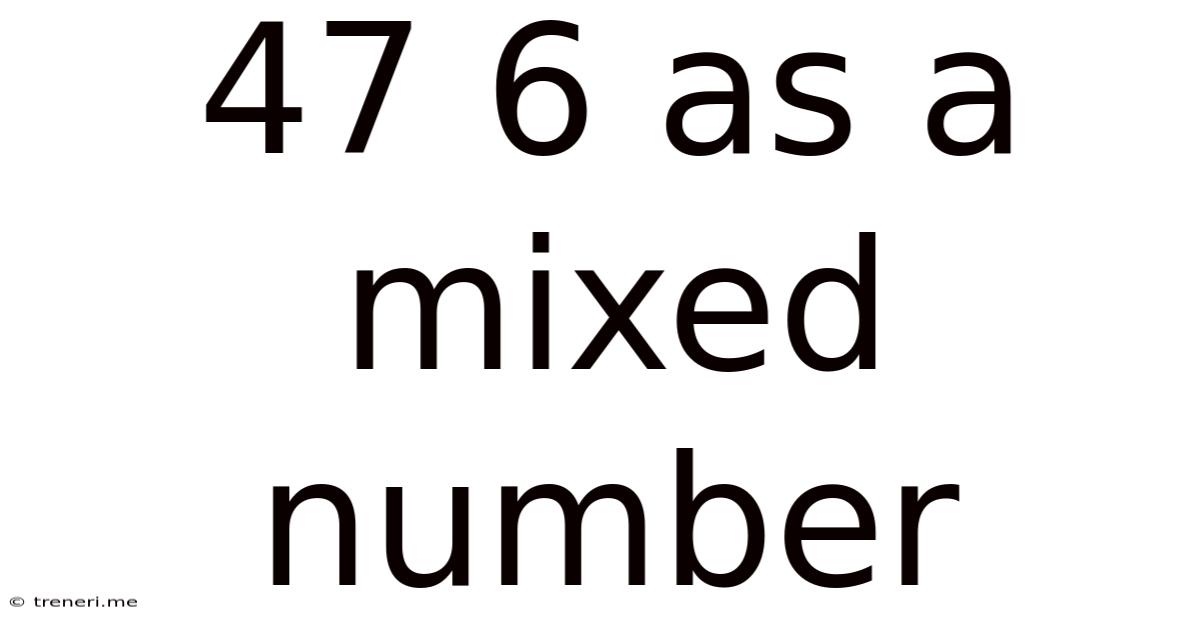
Table of Contents
47/6 as a Mixed Number: A Comprehensive Guide
Understanding how to convert an improper fraction, like 47/6, into a mixed number is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 47/6 but will also delve into the underlying concepts, provide various methods for solving similar problems, and offer practical applications to solidify your understanding. We'll explore this topic thoroughly, covering everything from the basic principles to advanced techniques.
Understanding Improper Fractions and Mixed Numbers
Before diving into the conversion process, let's define our key terms:
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and of course, our focus today, 47/6.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator is smaller than the denominator. Examples include 1 ¾, 2 ⅔, and the result we'll obtain from converting 47/6.
The conversion from an improper fraction to a mixed number essentially represents the division of the numerator by the denominator. It shows how many whole units are contained within the fraction, along with the remaining fractional part.
Method 1: Long Division
The most straightforward method for converting 47/6 to a mixed number involves long division. This method is particularly useful for larger numbers and helps visualize the process clearly.
-
Divide the numerator by the denominator: We divide 47 by 6.
7 --- 6|47 42 --- 5 -
Identify the whole number: The quotient (the result of the division) is 7. This represents the whole number part of our mixed number.
-
Identify the remainder: The remainder is 5. This becomes the numerator of the fractional part.
-
Retain the original denominator: The denominator of the fraction in our mixed number remains the same as the original denominator (6).
-
Combine the whole number and the fraction: Therefore, 47/6 as a mixed number is 7 ⁵⁄₆.
Method 2: Repeated Subtraction
This method offers a more intuitive approach, especially for those who find long division challenging.
-
Subtract the denominator repeatedly from the numerator: We repeatedly subtract 6 from 47 until we reach a number less than 6.
47 - 6 = 41 41 - 6 = 35 35 - 6 = 29 29 - 6 = 23 23 - 6 = 17 17 - 6 = 11 11 - 6 = 5
-
Count the number of subtractions: We performed 7 subtractions before reaching a remainder less than 6. This number (7) becomes the whole number part of our mixed number.
-
The remainder becomes the numerator: The remaining number, 5, is the numerator of the fraction.
-
Retain the original denominator: The denominator remains 6.
-
Combine the whole number and the fraction: Again, we arrive at the mixed number 7 ⁵⁄₆.
Method 3: Using Multiplication and Subtraction (A shortcut for larger numbers)
For very large improper fractions, this method can offer a slightly faster approach. It involves finding the closest multiple of the denominator to the numerator.
-
Estimate the whole number: We notice that 6 multiplied by 7 is 42, which is close to 47. This suggests our whole number will be close to 7.
-
Multiply the whole number estimate by the denominator: 7 * 6 = 42.
-
Subtract this product from the numerator: 47 - 42 = 5. This is our remainder.
-
Form the mixed number: The remainder (5) becomes the numerator, the original denominator (6) remains unchanged, and the estimated whole number (7) forms the whole number part.
-
Result: We get the mixed number 7 ⁵⁄₆.
Why is Understanding Mixed Numbers Important?
The ability to convert improper fractions to mixed numbers is crucial for several reasons:
-
Real-World Applications: Many real-world scenarios involve quantities expressed as mixed numbers. Think of measuring ingredients in a recipe (2 ½ cups of flour), expressing time (1 ¾ hours), or dealing with lengths and distances (3 ⅓ feet).
-
Simplifying Calculations: Mixed numbers are often easier to visualize and work with in calculations involving addition, subtraction, multiplication, or division compared to their improper fraction counterparts.
-
Problem-Solving: Converting to mixed numbers often provides a more intuitive understanding of the quantity represented by the improper fraction. It allows for easier comparisons and a better grasp of the problem’s scale.
Practice Problems
To solidify your understanding, let's try a few more examples. Convert the following improper fractions to mixed numbers:
- 23/4
- 31/7
- 50/12
- 97/11
- 125/8
(Solutions are provided at the end of the article.)
Advanced Applications
While converting improper fractions to mixed numbers may seem like a basic skill, it forms the foundation for many more advanced mathematical concepts, including:
-
Algebra: Understanding fractional notation and operations is crucial for solving algebraic equations that involve fractions.
-
Geometry: When dealing with area and volume calculations, you often encounter fractions that need to be converted to mixed numbers for easier interpretation of the results.
-
Calculus: Fractional representations and their manipulation are critical elements in calculus and other higher-level mathematics.
Conclusion
Converting an improper fraction, such as 47/6, to a mixed number is a foundational skill in mathematics. By understanding the different methods—long division, repeated subtraction, and the shortcut method—you can confidently handle various scenarios. Remember that this skill isn't just about rote memorization; it's about developing a deeper understanding of fractions and their representation in real-world situations.
Solutions to Practice Problems:
- 23/4 = 5 ¾
- 31/7 = 4 ³/₇
- 50/12 = 4 2/12 = 4 1/6 (simplified)
- 97/11 = 8 ⁹⁄₁₁
- 125/8 = 15 ⁵⁄₈
This comprehensive guide provides a thorough understanding of converting 47/6 into a mixed number, along with practical applications and additional practice problems to reinforce learning. Remember to practice regularly to master this essential mathematical skill!
Latest Posts
Latest Posts
-
Calculate How Much Heat Will Be Released Or Absorbed
May 15, 2025
-
What Is The Least Common Multiple Of 24 And 9
May 15, 2025
-
Cuanto Es 54 Grados Fahrenheit En Grados Celsius
May 15, 2025
-
Round 149 To The Nearest Hundred
May 15, 2025
-
Round 156 To The Nearest Hundred
May 15, 2025
Related Post
Thank you for visiting our website which covers about 47 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.