49 6 As A Mixed Number
Treneri
May 12, 2025 · 5 min read
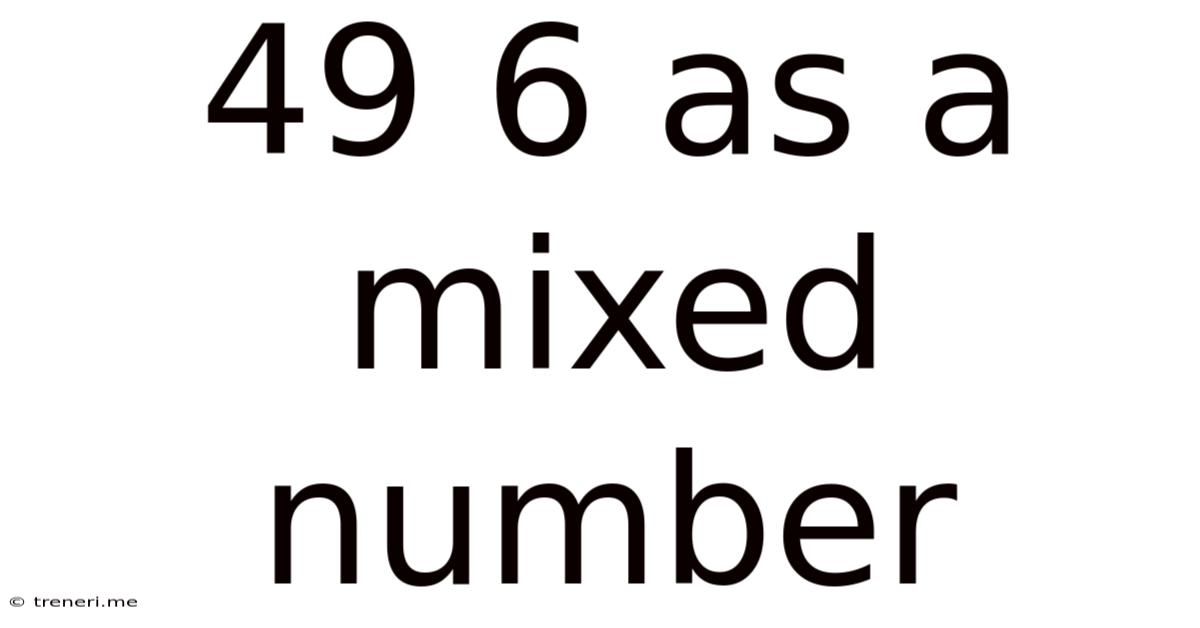
Table of Contents
49/6 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the improper fraction 49/6 into a mixed number, explaining the steps involved, providing practical examples, and exploring related concepts. We'll also touch upon the significance of understanding this conversion in various mathematical contexts.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit. Improper fractions, on the other hand, have a numerator that is greater than or equal to the denominator, such as 11/4.
Converting an Improper Fraction to a Mixed Number: The Process
The core process of converting an improper fraction to a mixed number involves division. Let's illustrate this using the example of 49/6.
Step 1: Divide the Numerator by the Denominator
Divide the numerator (49) by the denominator (6).
49 ÷ 6 = 8 with a remainder of 1
Step 2: Identify the Whole Number and the Remainder
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 8.
The remainder becomes the numerator of the fractional part of the mixed number. Here, the remainder is 1.
Step 3: Construct the Mixed Number
The denominator of the fractional part remains the same as the denominator of the original improper fraction (6).
Therefore, 49/6 as a mixed number is 8 1/6.
Visualizing the Conversion
Imagine you have 49 cookies, and you want to divide them equally among 6 friends. You can give each friend 8 cookies (8 x 6 = 48 cookies). You'll have 1 cookie left over. This leftover cookie represents the fraction 1/6. Thus, you've given each friend 8 whole cookies and 1/6 of a cookie, representing the mixed number 8 1/6.
Practical Applications of Converting Improper Fractions to Mixed Numbers
Understanding how to convert improper fractions to mixed numbers is crucial in various real-world scenarios and mathematical problems:
-
Measurement: When measuring lengths, weights, or volumes, you often encounter situations where the measurement involves a whole number and a fraction. For example, a piece of wood might be 5 3/8 inches long.
-
Baking and Cooking: Recipes often involve fractions of cups or teaspoons of ingredients. Converting improper fractions to mixed numbers makes it easier to understand and measure the required quantities accurately. Imagine a recipe calling for 17/4 cups of flour. Converting this to 4 ¼ cups makes it easier to measure.
-
Time: Representing time often involves mixed numbers. For instance, 1 hour and 20 minutes can be represented as 1 1/3 hours (20 minutes is 1/3 of an hour).
-
Geometry and Area Calculations: Solving geometry problems frequently requires working with fractions and mixed numbers, particularly when calculating areas or volumes.
Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
Once you have converted an improper fraction to a mixed number, you can use it in various mathematical operations. However, it's often easier to work with mixed numbers in some operations and improper fractions in others.
Addition and Subtraction: When adding or subtracting mixed numbers, it is often convenient to convert them into improper fractions first to streamline the calculation.
Multiplication and Division: While you can convert mixed numbers to improper fractions for multiplication and division, it's sometimes more efficient to work directly with the mixed numbers, especially in division.
Further Exploration of Fractions and Mixed Numbers
Here are some related concepts that are worth exploring further to solidify your understanding:
-
Equivalent Fractions: Understanding equivalent fractions helps you simplify fractions and find common denominators when adding or subtracting. For example, 1/2, 2/4, and 3/6 are all equivalent fractions.
-
Simplifying Fractions: Simplifying fractions, also known as reducing fractions, involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. This makes the fraction easier to work with. For example, 12/18 can be simplified to 2/3 by dividing both the numerator and the denominator by 6.
-
Comparing Fractions: Knowing how to compare fractions is essential when solving problems involving inequalities or ordering fractions. This involves using common denominators or comparing the fractions to benchmarks like 1/2 or 1.
-
Decimals and Fractions: Understanding the relationship between decimals and fractions is crucial for solving many mathematical problems. Converting between decimals and fractions (and mixed numbers) is a skill that requires practice and understanding.
Practice Problems
To solidify your understanding of converting improper fractions to mixed numbers, try converting the following improper fractions:
- 25/4
- 37/8
- 51/10
- 65/12
Solutions:
- 25/4 = 6 ¼
- 37/8 = 4 5/8
- 51/10 = 5 1/10
- 65/12 = 5 5/12
Conclusion
Converting improper fractions to mixed numbers is a crucial skill in mathematics with wide-ranging applications. By understanding the process of division, identifying whole numbers and remainders, and constructing the mixed number, you can effectively handle various mathematical problems involving fractions and mixed numbers. Mastering this skill provides a strong foundation for tackling more complex mathematical concepts and solving real-world problems involving fractions. Remember to practice regularly to enhance your proficiency and confidence in working with fractions and mixed numbers. The more you practice, the easier it will become.
Latest Posts
Latest Posts
-
Whats The Best Uv Index For Tanning
May 12, 2025
-
How Many Cups In 32 Ounces Of Liquid
May 12, 2025
-
8 Cups Is How Many Fluid Ounces
May 12, 2025
-
5 Cm Equals How Many Meters
May 12, 2025
-
How Many Sig Figs In 12 0
May 12, 2025
Related Post
Thank you for visiting our website which covers about 49 6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.