5/3 Divided By 2 In Fraction
Treneri
May 12, 2025 · 5 min read
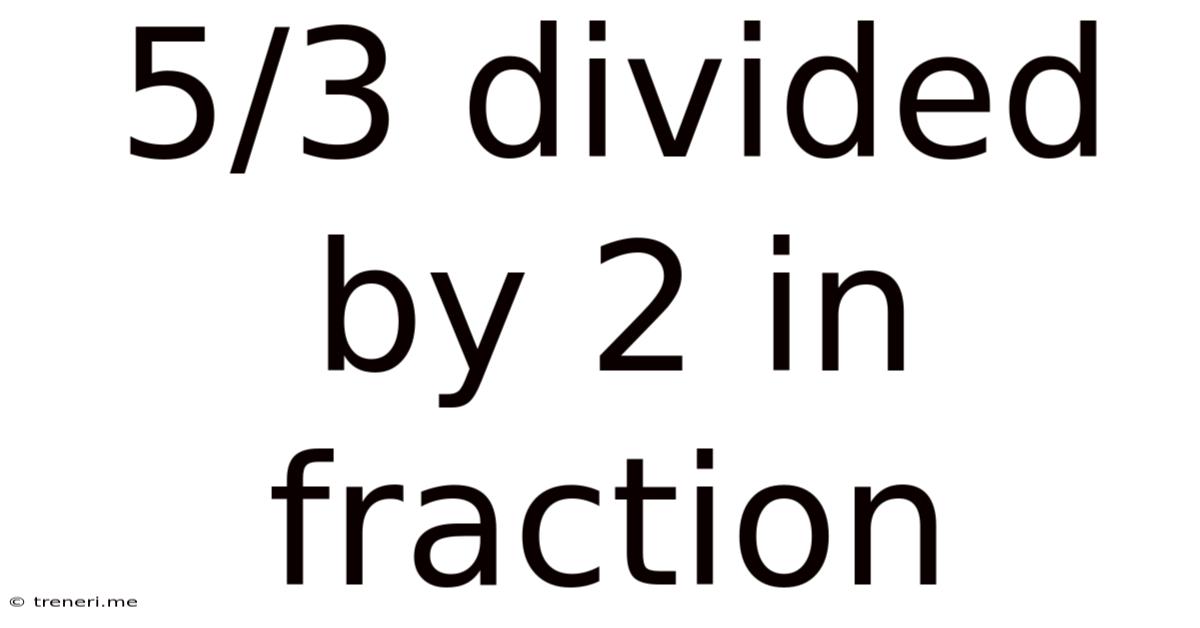
Table of Contents
5/3 Divided by 2: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will delve into the division of the fraction 5/3 by 2, explaining the steps involved, providing alternative approaches, and exploring related concepts to solidify your understanding of fraction manipulation.
Understanding Fraction Division
Before tackling the specific problem of 5/3 divided by 2, let's establish the fundamental principles of fraction division. The core concept is to invert the second fraction (the divisor) and multiply. This is because division is essentially the inverse operation of multiplication. Think of it this way: dividing by 2 is the same as multiplying by 1/2.
Key Principle: a/b ÷ c/d = a/b * d/c
Solving 5/3 Divided by 2
Now, let's apply this principle to our problem: 5/3 divided by 2. First, we need to express 2 as a fraction. Any whole number can be written as a fraction with a denominator of 1. Therefore, 2 can be written as 2/1.
Our problem now becomes: 5/3 ÷ 2/1
Following the rule of inverting and multiplying, we get:
5/3 * 1/2
Now, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(5 * 1) / (3 * 2) = 5/6
Therefore, 5/3 divided by 2 equals 5/6.
Alternative Methods and Visualizations
While the "invert and multiply" method is the most efficient, let's explore alternative approaches that can enhance understanding.
Method 1: Using the Reciprocal
The reciprocal of a number is simply 1 divided by that number. The reciprocal of 2 is 1/2. Dividing by 2 is the same as multiplying by its reciprocal, 1/2. This leads us back to the same calculation:
5/3 * 1/2 = 5/6
Method 2: Visual Representation with Fraction Bars
Imagine a bar representing 5/3. To divide this by 2, we need to split this 5/3 bar into two equal parts. Each part will represent (5/3) / 2. Visually, this reinforces the concept of dividing the fraction. Although difficult to precisely draw, this visualization aids in grasping the underlying concept. The result, as we've already calculated, is 5/6.
Simplifying Fractions: A Crucial Step
After performing any fraction operation, it's crucial to simplify the result to its lowest terms. In our case, 5/6 is already in its simplest form because 5 and 6 share no common factors other than 1. However, if we had obtained a fraction like 10/12, we would simplify it by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2 in this case: 10/12 simplifies to 5/6.
Expanding the Concept: Dividing Fractions with Mixed Numbers
Let's expand our understanding by tackling a similar problem involving mixed numbers. Suppose we need to solve 2 1/3 divided by 2.
Step 1: Convert Mixed Numbers to Improper Fractions
First, convert the mixed number 2 1/3 into an improper fraction. To do this, multiply the whole number (2) by the denominator (3) and add the numerator (1). The result becomes the new numerator, and the denominator remains the same:
(2 * 3) + 1 = 7 So, 2 1/3 becomes 7/3.
Step 2: Apply the Division Rule
Now, we have 7/3 ÷ 2/1. Following the "invert and multiply" rule:
7/3 * 1/2 = 7/6
Step 3: Simplify (if necessary)
7/6 is an improper fraction (the numerator is larger than the denominator). We can convert it to a mixed number:
7/6 = 1 1/6
Therefore, 2 1/3 divided by 2 equals 7/6 or 1 1/6.
Real-World Applications of Fraction Division
Understanding fraction division isn't just an academic exercise; it has practical applications in various real-world scenarios:
- Cooking and Baking: Dividing ingredients in recipes often involves fractions. If a recipe calls for 2 1/2 cups of flour and you want to halve the recipe, you'll need to divide this quantity by 2.
- Sewing and Crafting: Cutting fabric or other materials to specific sizes requires precise measurements, often involving fractions.
- Construction and Engineering: Many calculations in these fields involve fractions, requiring division to determine accurate dimensions and quantities.
- Data Analysis: Interpreting data often involves working with fractions and ratios, which necessitates division.
Troubleshooting Common Mistakes
Many students struggle with fraction division due to common errors:
- Forgetting to invert the divisor: This is the most frequent mistake. Remember the crucial step of inverting (flipping) the second fraction before multiplying.
- Incorrect multiplication of fractions: Ensure you correctly multiply the numerators and the denominators separately.
- Failing to simplify the final answer: Always simplify the resulting fraction to its lowest terms to obtain the most accurate and concise answer.
Practice Problems
To solidify your understanding, try solving these practice problems:
- 7/4 ÷ 3/2
- 3 1/2 ÷ 5
- 1/8 ÷ 1/4
- 9/5 ÷ 3
- 2 2/5 ÷ 1 1/2
By working through these examples and using the techniques explained in this guide, you'll build confidence and proficiency in dividing fractions. Remember to always check your work and simplify your answers. Consistent practice is key to mastering this essential mathematical skill. Don't hesitate to revisit the steps and explanations provided here as needed to further strengthen your understanding of fraction division. With focused practice and attention to detail, you'll confidently tackle any fraction division problem.
Latest Posts
Latest Posts
-
Radian Measure Of The Central Angle
May 15, 2025
-
Del 81 Al 2024 Cuantos Anos Son
May 15, 2025
-
How Much Does A Teaspoon Of Yeast Weigh
May 15, 2025
-
7 10 As A Mixed Number
May 15, 2025
-
Ab Welchem Uv Index Wird Man Braun
May 15, 2025
Related Post
Thank you for visiting our website which covers about 5/3 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.