5 6 Divided By 1 3 As A Fraction
Treneri
May 13, 2025 · 5 min read
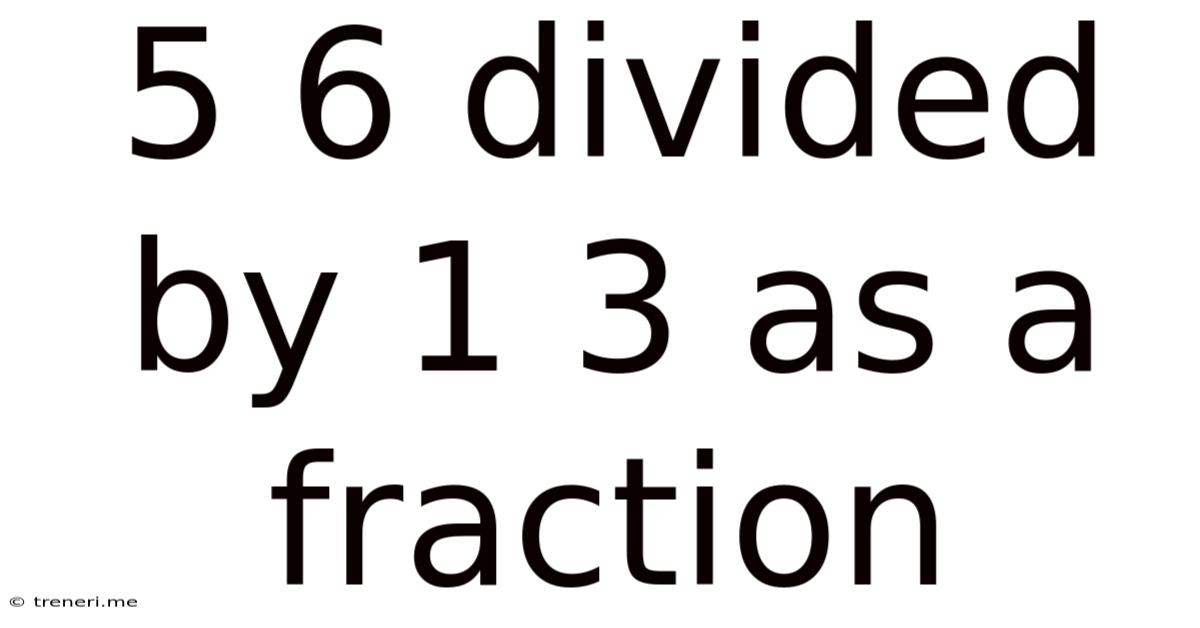
Table of Contents
5/6 Divided by 1/3 as a Fraction: A Comprehensive Guide
Understanding division with fractions can be tricky, but it's a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will walk you through the process of dividing 5/6 by 1/3, explaining the steps involved, providing alternative methods, and exploring related concepts. We'll also delve into the practical applications of fractional division and how it's used in everyday life and various fields.
Understanding Fraction Division
Before tackling the specific problem of 5/6 divided by 1/3, let's review the fundamental principles of fraction division. The key concept to grasp is that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/3 is 3/1 (or simply 3).
This principle allows us to convert a division problem into a multiplication problem, making the calculation significantly easier. This is because multiplying fractions is generally simpler than dividing them.
Calculating 5/6 Divided by 1/3
Now, let's apply this principle to our problem: 5/6 ÷ 1/3.
Step 1: Find the reciprocal of the second fraction.
The reciprocal of 1/3 is 3/1.
Step 2: Change the division sign to a multiplication sign.
Our problem now becomes: 5/6 × 3/1.
Step 3: Multiply the numerators (top numbers) together.
5 × 3 = 15
Step 4: Multiply the denominators (bottom numbers) together.
6 × 1 = 6
Step 5: Simplify the resulting fraction.
Our initial result is 15/6. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 3.
15 ÷ 3 = 5 6 ÷ 3 = 2
Therefore, the simplified answer is 5/2. This can also be expressed as a mixed number: 2 1/2.
Alternative Methods
While the reciprocal method is generally the most efficient, there are alternative approaches to solving this problem. Understanding these alternative methods can provide a deeper comprehension of fractional division.
Method 2: Using a Common Denominator
This method involves finding a common denominator for both fractions before performing the division. While longer than the reciprocal method, it highlights the underlying concept of division as finding how many times one fraction fits into another.
Step 1: Find a common denominator.
The least common denominator (LCD) for 6 and 3 is 6.
Step 2: Convert the fractions to equivalent fractions with the common denominator.
5/6 remains the same. 1/3 becomes 2/6 (multiply both numerator and denominator by 2).
Step 3: Perform the division.
Now we divide 5/6 by 2/6. This is equivalent to asking "How many times does 2/6 fit into 5/6?" We can simply divide the numerators: 5 ÷ 2 = 2.5.
Since both fractions have the same denominator, this gives us a result of 2.5. This can be converted back into a fraction by expressing 2.5 as 5/2.
Method 3: Visual Representation
Visualizing fractions can be particularly helpful for understanding the concept of division. Imagine you have a pizza cut into 6 slices (representing 5/6). You want to know how many 1/3 portions (which are equivalent to 2 slices) are in your 5/6 portion. You can see that 2 and a half 1/3 portions fit into the 5/6 portion. This visual approach reinforces the answer of 2 1/2 or 5/2.
Practical Applications of Fractional Division
Fractional division isn't just an abstract mathematical concept; it has numerous practical applications in everyday life and various professions.
-
Cooking and Baking: Recipes often require adjusting ingredient amounts. If a recipe calls for 1/3 cup of sugar and you only want to make half the recipe, you need to divide 1/3 by 2 (or multiply by 1/2), resulting in 1/6 cup of sugar.
-
Sewing and Tailoring: Calculating fabric requirements often involves working with fractions. If a pattern calls for 2/3 yards of fabric and you need to make three dresses, you need to multiply 2/3 by 3 to determine the total fabric needed.
-
Construction and Engineering: Dividing fractions is crucial in tasks involving measurements and proportions. Precise calculations are essential to ensure structural integrity.
-
Finance: Dividing fractions is used in calculations involving interest rates, loan repayments, and asset allocation.
-
Data Analysis: Fractional division is extensively used in statistical analysis, probability calculations, and data normalization.
-
Science: Many scientific calculations, particularly in chemistry and physics, involve working with fractions and performing divisions.
Further Exploration: Complex Fractions
Understanding fractional division forms a solid foundation for tackling more complex fractions. A complex fraction is a fraction where the numerator or denominator (or both) contains a fraction itself. For example: (5/6) / (1/3). Notice that this is the same problem we just solved, demonstrating that complex fractions can be simplified using the principles we’ve discussed. Solving complex fractions often involves a combination of simplifying the internal fractions and then using the reciprocal method to perform the division.
Conclusion: Mastering Fractional Division
Mastering fractional division is essential for success in mathematics and numerous practical applications. By understanding the reciprocal method, alternative approaches, and visual representations, you can confidently solve fraction division problems and appreciate their significance in various fields. The process of dividing 5/6 by 1/3, resulting in 5/2 or 2 1/2, serves as a clear example of the techniques and their real-world utility. Remember to practice regularly to strengthen your understanding and build proficiency. The more you work with fractions, the easier they become to manipulate and understand. This will ultimately improve your problem-solving skills and expand your mathematical capabilities.
Latest Posts
Latest Posts
-
What Set Of Side Lengths Form A Right Triangle
May 13, 2025
-
Cuanto Tarda Una Perra En Parir
May 13, 2025
-
180 Days From April 11 2024
May 13, 2025
-
What Is 1 5 2 3
May 13, 2025
-
90 Days From March 24 2024
May 13, 2025
Related Post
Thank you for visiting our website which covers about 5 6 Divided By 1 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.