5/6 Divided By 1/6 As A Fraction
Treneri
May 14, 2025 · 4 min read
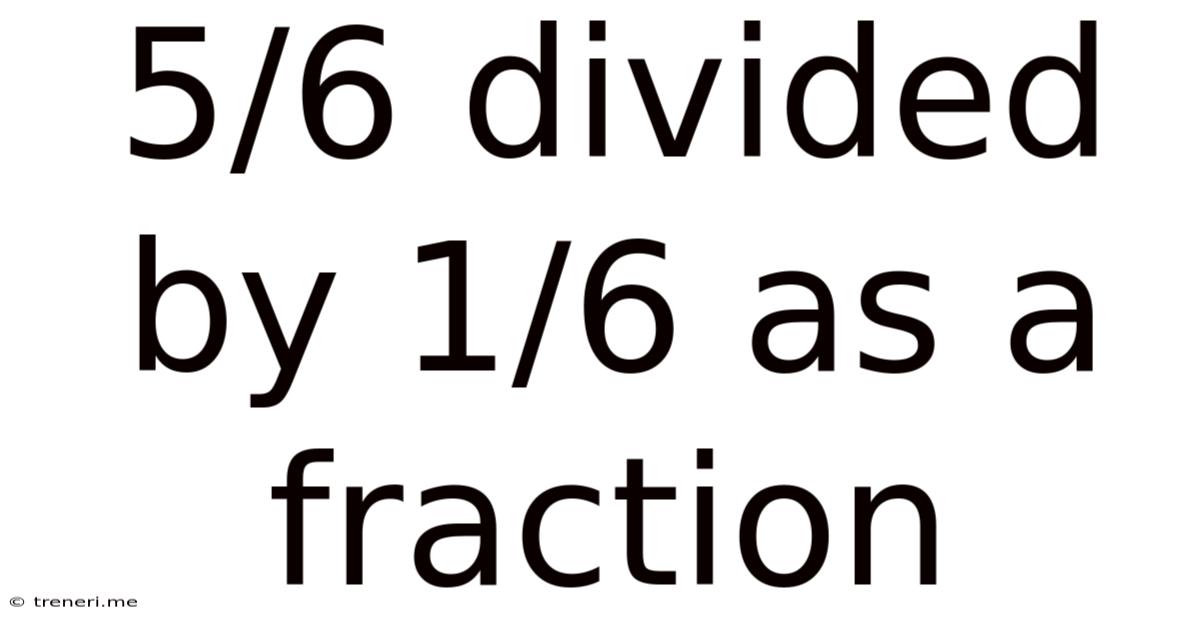
Table of Contents
5/6 Divided by 1/6 as a Fraction: A Deep Dive into Fraction Division
Understanding fraction division can be a stumbling block for many, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will break down how to solve 5/6 divided by 1/6, explaining the process step-by-step and exploring the underlying concepts. We'll also delve into practical applications and related problems to solidify your understanding. By the end, you'll not only know the answer but also possess the skills to tackle similar fraction division problems with confidence.
Understanding Fraction Division
Before tackling the specific problem of 5/6 ÷ 1/6, let's establish a strong foundation in fraction division. The core principle is to invert the second fraction (the divisor) and multiply. This is also known as the "keep, change, flip" method.
The "Keep, Change, Flip" Method
This simple mnemonic device helps remember the steps involved:
- Keep: Keep the first fraction as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (or invert) the second fraction. This means switching the numerator and the denominator.
For example, if we have a/b ÷ c/d, the process becomes:
a/b × d/c
Now, let's apply this to our problem.
Solving 5/6 Divided by 1/6
Our problem is 5/6 ÷ 1/6. Following the "keep, change, flip" method:
- Keep: We keep the first fraction, 5/6, as it is.
- Change: We change the division sign (÷) to a multiplication sign (×).
- Flip: We flip the second fraction, 1/6, to become 6/1.
This transforms the problem into:
5/6 × 6/1
Now we can perform the multiplication:
(5 × 6) / (6 × 1) = 30 / 6
Finally, we simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 6:
30 ÷ 6 / 6 ÷ 6 = 5/1
Therefore, 5/6 ÷ 1/6 = 5
Visualizing the Problem
Understanding fraction division visually can be incredibly helpful. Imagine you have 5/6 of a pizza. You want to divide this 5/6 into portions that are each 1/6 of the pizza. How many portions will you have? The answer, as we've calculated, is 5. Each 1/6 slice is a portion, and you have 5 of them in your 5/6 of a pizza.
Working with Different Fractions
Let's explore other examples to further solidify your understanding of fraction division.
Example 1: 3/4 ÷ 1/2
- Keep: 3/4
- Change: ÷ becomes ×
- Flip: 1/2 becomes 2/1
3/4 × 2/1 = (3 × 2) / (4 × 1) = 6/4
Simplifying: 6/4 = 3/2 or 1 ½
Example 2: 2/3 ÷ 5/6
- Keep: 2/3
- Change: ÷ becomes ×
- Flip: 5/6 becomes 6/5
2/3 × 6/5 = (2 × 6) / (3 × 5) = 12/15
Simplifying: 12/15 = 4/5
Example 3: 1/8 ÷ 3/4
- Keep: 1/8
- Change: ÷ becomes ×
- Flip: 3/4 becomes 4/3
1/8 × 4/3 = (1 × 4) / (8 × 3) = 4/24
Simplifying: 4/24 = 1/6
Real-World Applications of Fraction Division
Fraction division isn't just a theoretical concept; it has numerous practical applications in everyday life:
- Cooking: Dividing recipes to adjust serving sizes. If a recipe calls for 2/3 cup of flour and you want to make half the recipe, you'd use 2/3 ÷ 2 = 1/3 cup of flour.
- Sewing: Calculating fabric requirements. If you need 3/4 of a yard of fabric for one item and want to make three, you'd calculate 3/4 × 3 = 2 ¼ yards.
- Construction: Measuring and cutting materials. Dividing lengths of wood or pipes accurately.
- Finance: Calculating portions of a budget or sharing expenses.
- Science: Many scientific calculations and conversions involve fractions and their division.
Troubleshooting Common Mistakes
Here are some common pitfalls to watch out for when dividing fractions:
- Forgetting to flip the second fraction: This is the most frequent error. Remember the "keep, change, flip" rule.
- Incorrect simplification: Always reduce the resulting fraction to its simplest form by finding the greatest common divisor of the numerator and denominator.
- Multiplying instead of dividing: Make sure you understand the difference and apply the correct method.
- Incorrect multiplication of fractions: Remember to multiply numerators together and denominators together.
Conclusion
Mastering fraction division is a fundamental skill with widespread applications. By understanding the "keep, change, flip" method, practicing various examples, and visualizing the process, you can confidently tackle fraction division problems. Remember to always simplify your answer to its lowest terms. With consistent practice, fraction division will become second nature, empowering you to solve more complex mathematical problems and apply this crucial skill to real-world situations. The solution to 5/6 ÷ 1/6, as we've thoroughly explored, is 5. Now you have the tools to conquer similar challenges with ease and accuracy.
Latest Posts
Latest Posts
-
Cuantos Dias Faltan Para El 16 De Enero
May 15, 2025
-
How Much Is A Half A Pound In Grams
May 15, 2025
-
Reduce 24 40 To Its Lowest Terms
May 15, 2025
-
How To Calculate Cbm For Sea Shipment
May 15, 2025
-
150 Cm Is How Many Meters
May 15, 2025
Related Post
Thank you for visiting our website which covers about 5/6 Divided By 1/6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.