5/6 Divided By 2/7 As A Fraction
Treneri
May 13, 2025 · 5 min read
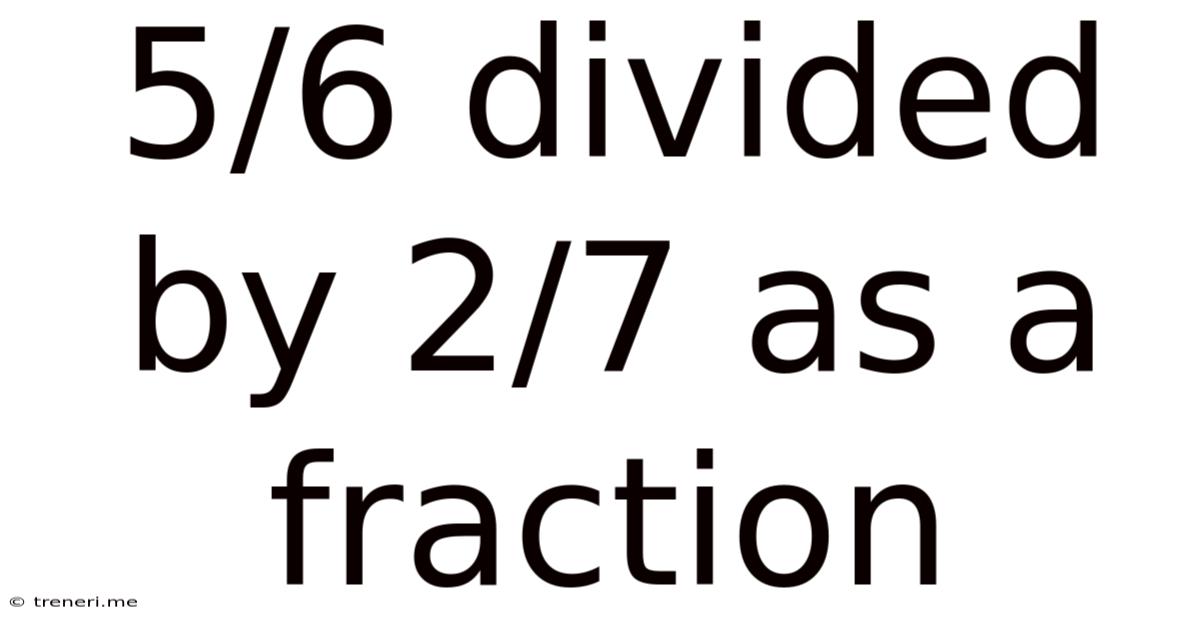
Table of Contents
5/6 Divided by 2/7 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This comprehensive guide will walk you through dividing 5/6 by 2/7, explaining the steps involved, providing alternative methods, and exploring related concepts to solidify your understanding of fraction division.
Understanding Fraction Division
Before diving into the specific problem, let's refresh our understanding of dividing fractions. The core principle is to invert the second fraction (the divisor) and multiply. This means flipping the numerator and denominator of the second fraction. So, dividing by a fraction is equivalent to multiplying by its reciprocal.
This method stems from the fundamental definition of division: a ÷ b = a × (1/b). When 'b' is a fraction, say x/y, then a ÷ (x/y) = a × (y/x). This explains why we invert and multiply.
Solving 5/6 Divided by 2/7
Now, let's tackle the problem at hand: 5/6 ÷ 2/7.
Following the rule of inverting and multiplying, we transform the division problem into a multiplication problem:
(5/6) × (7/2)
Next, we multiply the numerators together and the denominators together:
(5 × 7) / (6 × 2) = 35/12
Therefore, 5/6 divided by 2/7 equals 35/12. This is an improper fraction, meaning the numerator is larger than the denominator.
Converting to Mixed Number
Improper fractions are often converted into mixed numbers for easier interpretation. A mixed number consists of a whole number and a proper fraction. To convert 35/12 to a mixed number, we perform division:
35 ÷ 12 = 2 with a remainder of 11.
This means 35/12 can be expressed as 2 11/12.
Therefore, 5/6 divided by 2/7 is equivalent to both 35/12 and 2 11/12. Both answers are correct, and the choice between them depends on the context and preferred representation.
Alternative Methods for Dividing Fractions
While the invert-and-multiply method is the most common and efficient, let's explore some alternative approaches that can enhance your understanding.
Method 1: Using Common Denominators
This method involves finding a common denominator for both fractions before performing the division. While less efficient than the invert-and-multiply method for simple problems, it offers a different perspective and can be useful in more complex scenarios.
First, find the least common multiple (LCM) of the denominators 6 and 7. The LCM of 6 and 7 is 42.
Next, convert both fractions to have a denominator of 42:
5/6 = (5 × 7) / (6 × 7) = 35/42
2/7 = (2 × 6) / (7 × 6) = 12/42
Now, perform the division:
(35/42) ÷ (12/42) = 35/12
Notice that this yields the same result as the invert-and-multiply method. This method is more computationally intensive but helps visualize the division process differently.
Method 2: Visual Representation using Models
Visual aids can be exceptionally helpful, particularly when explaining fraction division to beginners. Imagine representing 5/6 with a rectangle divided into 6 equal parts, 5 of which are shaded. Dividing this by 2/7 means figuring out how many groups of 2/7 fit into 5/6. This approach, while less practical for complex calculations, offers a strong intuitive grasp of the concept.
Creating visual models to represent fractions and their division can be a beneficial approach, especially for visual learners and those new to the concept of fraction division.
Simplifying Fractions: A Crucial Step
After performing any fraction operation, it's crucial to simplify the result to its lowest terms. Simplification involves dividing both the numerator and the denominator by their greatest common divisor (GCD).
In our example, 35/12 is already in its simplest form because the GCD of 35 and 12 is 1. However, if we had obtained a fraction like 6/12, we would simplify it to 1/2 by dividing both the numerator and denominator by 6 (their GCD).
Practical Applications of Fraction Division
Fraction division finds applications in numerous real-world scenarios. Here are some examples:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make only 1/3 of the recipe, you need to calculate (1/2) ÷ (3/1) = 1/6 cup of flour.
-
Sewing and Crafting: Cutting fabric or other materials often involves fractional measurements. Dividing fractions helps in accurately calculating the required lengths.
-
Construction and Engineering: Many construction projects rely on precise measurements involving fractions. Calculating material requirements, dividing spaces, and other tasks demand a strong understanding of fraction division.
-
Data Analysis: When working with datasets, especially when dealing with proportions or ratios, understanding fraction division is essential for analysis and interpretation.
-
Finance: Dividing shares or calculating portions of investments frequently uses fraction division.
Advanced Concepts Related to Fraction Division
Understanding fraction division lays the groundwork for more advanced mathematical concepts:
-
Rational Numbers: Fractions are rational numbers, numbers that can be expressed as a ratio of two integers. Mastering fraction division strengthens your understanding of rational number operations.
-
Algebra: Fraction division is a fundamental skill in algebra. Solving equations and simplifying algebraic expressions often requires dividing fractions.
-
Calculus: Calculus relies heavily on the concept of limits and derivatives, which involve intricate manipulations of fractions and the division of fractions.
-
Complex Numbers: While seemingly unrelated at first glance, the underlying principles of division extend to operations with complex numbers, involving both real and imaginary parts.
Conclusion
Dividing fractions, specifically 5/6 divided by 2/7, is a fundamental skill with significant practical implications. By mastering the invert-and-multiply method and understanding the underlying principles, you can confidently solve such problems and apply this knowledge to various situations. Remember to always simplify your answers to their lowest terms for clarity and accuracy. Through consistent practice and a deeper exploration of related concepts, your proficiency in fraction division will undoubtedly improve, paving the way for success in more advanced mathematical concepts. This understanding extends far beyond the classroom, making it a vital skill for numerous professions and everyday situations.
Latest Posts
Latest Posts
-
Formula De Grados Fahrenheit A Centigrados
May 14, 2025
-
How Many Percent Is 11 Out Of 15
May 14, 2025
-
Greatest Common Factor Of 25 And 55
May 14, 2025
-
What Is 10 Out Of 15 As A Grade
May 14, 2025
-
How To Calculate 80 Percent Of A Number
May 14, 2025
Related Post
Thank you for visiting our website which covers about 5/6 Divided By 2/7 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.