5 7 Divided By 1 3
Treneri
May 12, 2025 · 5 min read
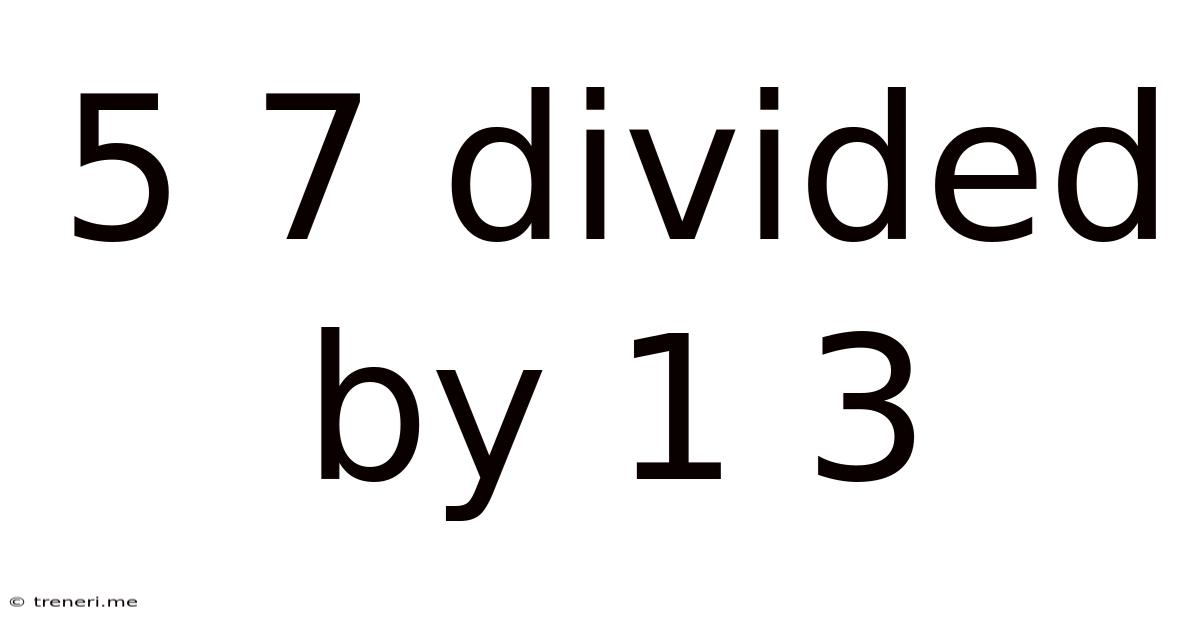
Table of Contents
Decoding the Division: A Deep Dive into 5 ⁷/₁₃ Divided by 1 ¹/₃
This seemingly simple division problem, 5 ⁷/₁₃ ÷ 1 ¹/₃, hides a surprising depth of mathematical concepts. While the answer itself might be quickly obtained with a calculator, understanding the underlying principles is crucial for building a strong foundation in mathematics and problem-solving. This article will not only solve the problem step-by-step but will also explore the various methods, explain the rationale behind each step, and delve into the broader mathematical context.
Understanding Mixed Numbers and Improper Fractions
Before tackling the division, let's solidify our understanding of mixed numbers and improper fractions. A mixed number, like 5 ⁷/₁₃, represents a whole number and a fraction combined. An improper fraction, on the other hand, is a fraction where the numerator (top number) is larger than or equal to the denominator (bottom number). For example, an improper fraction equivalent to 5 ⁷/₁₃ would be (5 x 13 + 7)/13 = 72/13.
Converting between mixed numbers and improper fractions is a fundamental skill in arithmetic. To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator; this becomes the new numerator, while the denominator remains the same. Conversely, to convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient becomes the whole number, and the remainder becomes the numerator of the fraction, with the denominator remaining unchanged.
Method 1: Converting to Improper Fractions
The most straightforward method to divide mixed numbers involves converting them into improper fractions. This simplifies the division process significantly.
Step 1: Convert the mixed numbers to improper fractions:
- 5 ⁷/₁₃ becomes (5 x 13 + 7)/13 = 72/13
- 1 ¹/₃ becomes (1 x 3 + 1)/3 = 4/3
Step 2: Rewrite the division as a multiplication:
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and the denominator.
Therefore, 72/13 ÷ 4/3 becomes 72/13 x 3/4
Step 3: Simplify and multiply:
Before multiplying, we can simplify the fractions by canceling common factors. Both 72 and 4 are divisible by 4:
72/4 = 18 and 4/4 = 1
Our expression now becomes:
18/13 x 3/1 = 54/13
Step 4: Convert back to a mixed number:
Finally, convert the improper fraction 54/13 back to a mixed number by dividing 54 by 13:
54 ÷ 13 = 4 with a remainder of 2.
Therefore, 54/13 = 4 ²/₁₃
Therefore, 5 ⁷/₁₃ ÷ 1 ¹/₃ = 4 ²/₁₃
Method 2: Using Long Division with Mixed Numbers
This method avoids converting to improper fractions but requires a more intricate long division process.
Step 1: Set up the long division:
Write the problem as a long division, placing the dividend (5 ⁷/₁₃) inside the division symbol and the divisor (1 ¹/₃) outside.
Step 2: Convert the divisor to a decimal:
Converting 1 ¹/₃ to a decimal is easier for long division. 1 ¹/₃ = 1.333... (recurring decimal). However, to avoid rounding errors, it's advisable to use a fraction-based approach whenever possible. We will maintain the fractional form in our calculation below for accuracy.
Step 3: Long division with fractions (Advanced Method):
This involves a series of subtractions using the divisor. While possible, this method is significantly more complex than converting to improper fractions and should be used only if specifically required. It involves repeated subtraction of 1 ¹/₃ from 5 ⁷/₁₃. This approach is prone to errors, especially with more complex mixed numbers.
Step 4: Convert the result back to a mixed number (if necessary):
The result obtained from long division should then be converted into a mixed number if it's not already in that form.
This method, although feasible, is less efficient and more prone to errors compared to the improper fraction method.
Understanding the Significance of the Result
The result, 4 ²/₁₃, signifies that 1 ¹/₃ goes into 5 ⁷/₁₃ approximately four times with a remainder. This remainder represents the portion of 5 ⁷/₁₃ that couldn't be evenly divided by 1 ¹/₃. Understanding remainders is essential in many practical applications, from distributing resources to calculating proportions.
Practical Applications and Real-World Scenarios
Division of mixed numbers finds application in various real-world scenarios:
- Cooking and Baking: Scaling recipes up or down often involves dividing mixed number quantities.
- Construction and Engineering: Calculating material quantities, dividing lengths, or determining proportions.
- Finance and Budgeting: Dividing budgets or allocating resources based on fractional shares.
- Science and Engineering: Many scientific calculations involve fractions and mixed numbers, particularly in fields like physics and chemistry.
Further Exploration: Decimal Approximations and Error Analysis
While the exact answer is 4 ²/₁₃, using decimal approximations can introduce errors. For example, if we approximate 5 ⁷/₁₃ as 5.54 and 1 ¹/₃ as 1.33, the result of the division will be slightly different from the exact answer obtained using fractions. Understanding the potential for rounding errors and their impact on the result is crucial for accuracy in calculations. This is especially important in fields where precision is paramount, such as engineering and scientific research.
Conclusion: Mastering Mixed Number Division
Dividing mixed numbers is a fundamental skill that builds upon a broader understanding of fractions, improper fractions, and long division. While a calculator can provide a quick answer, comprehending the underlying principles is vital for solving more complex problems and applying these skills to real-world situations. This detailed exploration of the division of 5 ⁷/₁₃ by 1 ¹/₃ highlights the importance of understanding multiple methods and the significance of accuracy in mathematical calculations. The choice of method often depends on personal preference and the complexity of the numbers involved, with the conversion to improper fractions generally providing the most efficient and least error-prone approach. By mastering these techniques, you build a solid foundation for tackling more advanced mathematical concepts and problem-solving endeavors.
Latest Posts
Latest Posts
-
How To Find Class Width Of A Histogram
May 13, 2025
-
Calculate Heat Capacity Of A Calorimeter
May 13, 2025
-
How Many Miles Is 450 Kilometers
May 13, 2025
-
Highest Common Factor Of 72 And 96
May 13, 2025
-
How To Do Diamond Problems In Math
May 13, 2025
Related Post
Thank you for visiting our website which covers about 5 7 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.