5 Divided By 1 6 As A Fraction
Treneri
May 11, 2025 · 5 min read
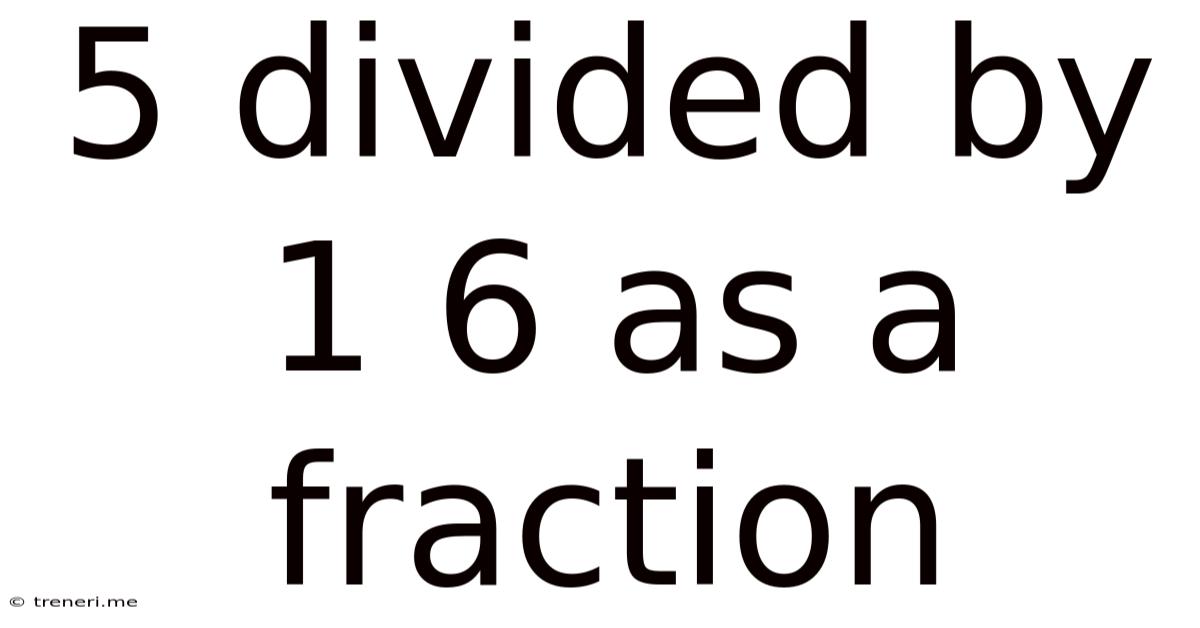
Table of Contents
5 Divided by 1 6 as a Fraction: A Comprehensive Guide
Understanding how to divide a whole number by a mixed fraction is a crucial skill in mathematics. This comprehensive guide will walk you through the process of calculating 5 divided by 1 6 as a fraction, explaining each step clearly and providing additional examples to reinforce your understanding. We'll also explore the broader context of dividing fractions and mixed numbers, covering key concepts and techniques.
Understanding the Problem: 5 ÷ 1 6
The problem "5 divided by 1 6" can be written mathematically as:
5 ÷ 1 6
This represents the division of a whole number (5) by a mixed number (1 6). Mixed numbers combine a whole number and a proper fraction. To solve this, we need to convert the mixed number into an improper fraction and then apply the rules of fraction division.
Converting Mixed Numbers to Improper Fractions
The first step is crucial: converting the mixed number 1 6 into an improper fraction. A mixed number represents a whole number plus a fraction. To convert it to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 6 = 6
- Add the numerator to the result: 6 + 1 = 7
- Keep the same denominator: The denominator remains 6.
Therefore, the improper fraction equivalent of 1 6 is 7/6.
Dividing Fractions: The Reciprocal Method
Dividing fractions involves a simple yet powerful technique: using the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 7/6 is 6/7.
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction. This rule applies even when one of the numbers is a whole number—we can represent a whole number as a fraction with a denominator of 1. In our case:
5 can be written as 5/1.
So, the problem becomes:
5/1 ÷ 7/6
Now, we apply the reciprocal method:
5/1 * 6/7
This simplifies to:
(5 * 6) / (1 * 7) = 30/7
Simplifying the Resulting Fraction
The result, 30/7, is an improper fraction because the numerator (30) is larger than the denominator (7). We can convert this improper fraction into a mixed number to make it easier to understand. To do this:
- Divide the numerator by the denominator: 30 ÷ 7 = 4 with a remainder of 2.
- The quotient becomes the whole number: 4
- The remainder becomes the numerator: 2
- The denominator stays the same: 7
Therefore, 30/7 is equivalent to the mixed number 4 2/7.
The Complete Solution: 5 ÷ 1 6 = 4 2/7
Following all the steps, we find that 5 divided by 1 6 is equal to 4 2/7. This represents four whole units and two-sevenths of another unit.
Practical Applications and Real-World Examples
Understanding fraction division has many practical applications in everyday life and various professional fields. Here are a few examples:
- Cooking and Baking: Recipes often require dividing ingredients. For instance, if a recipe calls for 5 cups of flour and you want to make only 1 1/2 times the recipe, you’d need to divide 5 by 1 1/2.
- Construction and Measurement: Dividing lengths and quantities is essential in construction and engineering projects.
- Sewing and Tailoring: Dividing fabric lengths accurately is crucial for garment creation.
- Data Analysis and Statistics: Division of fractions is often involved in calculations related to proportions, percentages, and ratios.
Further Exploration of Fraction Operations
Let's delve deeper into the general rules and techniques related to fractions:
Adding and Subtracting Fractions
To add or subtract fractions, they must have a common denominator. If they don't, find the least common multiple (LCM) of the denominators and convert the fractions accordingly. Then, add or subtract the numerators while keeping the denominator the same.
Example: 1/3 + 2/5 = (5/15) + (6/15) = 11/15
Multiplying Fractions
Multiplying fractions is straightforward: multiply the numerators together and the denominators together. Simplify the resulting fraction if possible.
Example: 2/3 * 4/5 = (2 * 4) / (3 * 5) = 8/15
Simplifying Fractions
Simplifying a fraction involves reducing it to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Example: 12/18. The GCD of 12 and 18 is 6. Dividing both numerator and denominator by 6 results in 2/3.
Troubleshooting Common Mistakes
When working with fractions, several common mistakes can occur:
- Incorrect conversion of mixed numbers to improper fractions: Double-check your calculations when converting.
- Forgetting to find a common denominator when adding or subtracting: Remember this crucial step.
- Incorrectly applying the reciprocal when dividing: Make sure you're flipping the correct fraction.
- Failure to simplify fractions: Always simplify your answer to its lowest terms.
Practice Problems
To solidify your understanding, try these practice problems:
- 7 ÷ 2 1/3
- 3 1/2 ÷ 1 1/4
- 10 ÷ 2 1/5
- 4 2/3 ÷ 2
Conclusion
Understanding how to divide a whole number by a mixed fraction, as demonstrated with the example 5 ÷ 1 6, is an essential mathematical skill. By mastering the steps of converting mixed numbers to improper fractions and applying the reciprocal method for fraction division, you can confidently solve various problems involving fractions in numerous real-world applications. Remember to practice regularly and review the common mistakes to improve your accuracy and efficiency. The more you practice, the more comfortable and proficient you'll become in working with fractions.
Latest Posts
Latest Posts
-
Cual Es La Raiz Cuadrada De 12
May 13, 2025
-
120 Days From August 30 2024
May 13, 2025
-
60 Dollars With 30 Percent Off
May 13, 2025
-
How Much Is 2000 Cubic Feet
May 13, 2025
-
How Long Does It Take To Read 1200 Words
May 13, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 1 6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.