5 Is 10 Percent Of What Number
Treneri
May 12, 2025 · 5 min read
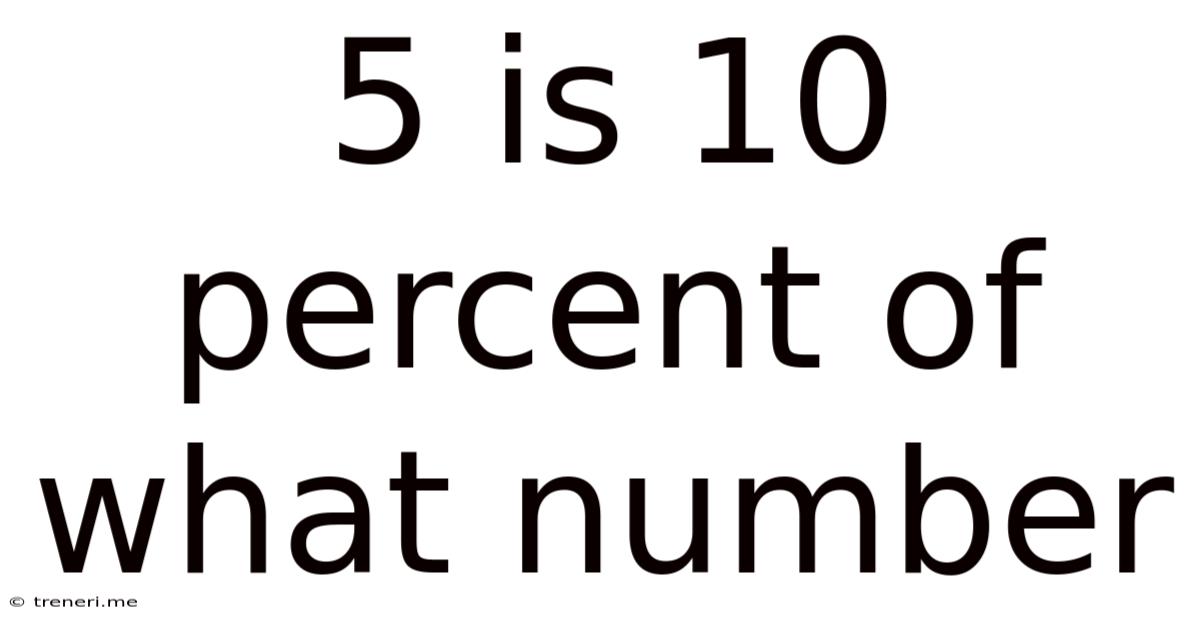
Table of Contents
5 is 10 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This comprehensive guide will delve into the question, "5 is 10 percent of what number?", exploring different methods to solve this type of problem and expanding on the broader concept of percentage calculations. We'll cover the fundamental principles, practical applications, and even touch upon more advanced scenarios.
Understanding Percentages: The Basics
Before diving into the specific problem, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred." For example, 10% means 10 out of 100, which can also be written as the fraction 10/100 or the decimal 0.10.
Key Concepts:
- Percentage: Represents a portion of a whole.
- Whole (or Base): The total amount or quantity from which the percentage is derived.
- Part: The portion of the whole represented by the percentage.
The relationship between these three elements can be expressed using the following formula:
(Part / Whole) x 100 = Percentage
This formula is crucial for solving percentage problems. We can rearrange this formula to solve for any of the three variables given the other two.
Solving "5 is 10 Percent of What Number?"
Now, let's tackle the central question: "5 is 10 percent of what number?" We can approach this problem using several methods:
Method 1: Using the Percentage Formula
We know the following:
- Part = 5
- Percentage = 10%
- Whole = x (This is what we need to find)
Let's plug these values into our percentage formula and solve for x:
(5 / x) x 100 = 10
Now, let's solve for x:
- Divide both sides by 100: (5 / x) = 0.1
- Multiply both sides by x: 5 = 0.1x
- Divide both sides by 0.1: x = 5 / 0.1
- Therefore, x = 50
So, 5 is 10 percent of 50.
Method 2: Using the Decimal Equivalent
We can also solve this using the decimal equivalent of 10%, which is 0.10. The problem can be rewritten as:
0.10 * x = 5
Solving for x:
x = 5 / 0.10
x = 50
Method 3: Using Proportions
Another approach is to set up a proportion:
5/x = 10/100
Cross-multiply:
10x = 500
Divide both sides by 10:
x = 50
Practical Applications: Real-World Scenarios
Understanding percentage calculations is vital in various real-world situations. Let's explore a few examples:
1. Sales and Discounts: Imagine a store offering a 10% discount on an item originally priced at $50. Using our knowledge, we can easily calculate the discount amount: 10% of $50 is $5. The final price after the discount would be $45.
2. Taxes: Suppose a sales tax rate is 10%, and you purchased an item for $5. The amount of tax you would pay is 10% of $5, which is $0.50. The total cost, including tax, would be $5.50.
3. Tip Calculations: If you want to leave a 10% tip on a meal costing $50, the tip amount would be 10% of $50, which is $5.
4. Financial Analysis: Percentage calculations are essential for analyzing financial statements. For example, you might calculate the percentage change in revenue from one year to the next.
5. Data Analysis and Statistics: Percentages are used extensively in statistical analysis to represent proportions, trends, and changes in data sets.
Advanced Percentage Calculations: Beyond the Basics
While the problem "5 is 10 percent of what number?" is relatively straightforward, let's consider some more complex scenarios:
1. Finding the Percentage Increase or Decrease: To calculate the percentage increase or decrease between two numbers, use the following formula:
[(New Value - Old Value) / Old Value] x 100
For instance, if the price of an item increased from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100 = 20%
2. Calculating Multiple Percentages: Sometimes, you need to apply multiple percentages consecutively. For example, a store might offer a 10% discount followed by an additional 5% discount. It's important to apply these discounts sequentially, not additively. A 10% discount on $100 is $10, leaving a price of $90. A 5% discount on $90 is $4.50, leaving a final price of $85.50. This is different from a 15% discount ($15), showing the importance of sequential calculation.
3. Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This is a more complex calculation but a crucial concept in finance. Formulas exist to calculate compound interest precisely.
4. Percentage Points vs. Percentages: It is crucial to differentiate between percentage points and percentages. A change from 10% to 15% is a 5-percentage-point increase, but a 50% increase relative to the original 10%. This distinction is often missed, leading to misinterpretations.
Tips and Tricks for Solving Percentage Problems
Here are some helpful tips to improve your proficiency in solving percentage problems:
- Master the formula: Thoroughly understand the fundamental percentage formula and how to rearrange it to solve for different variables.
- Use decimals: Converting percentages to decimals simplifies calculations.
- Practice regularly: Consistent practice is key to mastering any mathematical concept.
- Check your work: Always double-check your calculations to avoid errors.
- Utilize online calculators: While understanding the underlying principles is vital, online calculators can be used for verification or to tackle more complex calculations. However, always ensure the understanding of the methodology.
- Break down complex problems: Decompose complex percentage problems into smaller, manageable steps.
Conclusion
The question "5 is 10 percent of what number?" serves as an excellent starting point for understanding percentage calculations. By mastering the fundamental concepts and exploring different solution methods, you'll equip yourself with a valuable skill applicable across numerous fields. From everyday shopping to complex financial analysis, a solid understanding of percentages is indispensable. Remember to practice regularly and apply these principles to real-world scenarios to reinforce your learning and improve your problem-solving skills. The more you practice, the more confident and proficient you will become in tackling all manner of percentage calculations.
Latest Posts
Latest Posts
-
Can I Get Tan In Uv 5
May 14, 2025
-
500 Miles Equals How Many Kilometers
May 14, 2025
-
Does Elbow Macaroni Double In Size When Cooked
May 14, 2025
-
Cuanto Es El 10 De 200
May 14, 2025
-
How Long Is 65 Days In Months
May 14, 2025
Related Post
Thank you for visiting our website which covers about 5 Is 10 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.