5 Out Of 15 Is What Percent
Treneri
May 14, 2025 · 5 min read
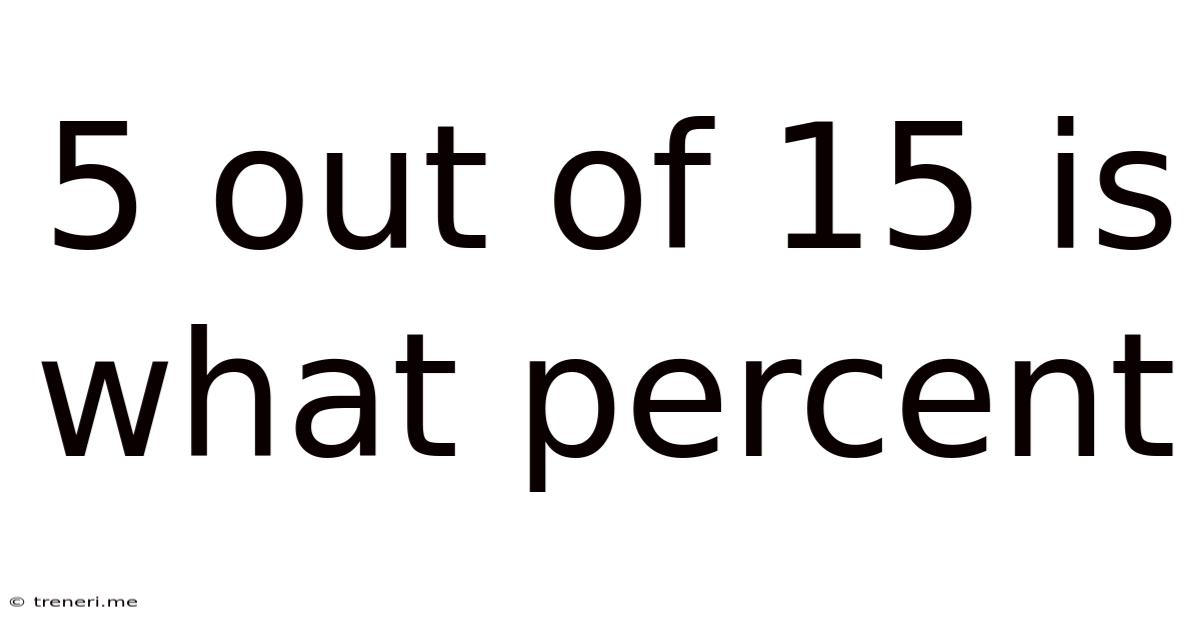
Table of Contents
5 out of 15 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only answer the question, "5 out of 15 is what percent?" but also equip you with the knowledge and techniques to tackle similar percentage problems with confidence. We'll explore various methods, delve into the underlying concepts, and provide practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." When we say "x percent," we mean x out of every 100. For instance, 50% means 50 out of 100, which is equivalent to one-half (½) or 0.5 as a decimal.
Key Concepts:
- Part: This represents the specific amount we're interested in (in our case, 5).
- Whole: This represents the total amount (in our case, 15).
- Percentage: This is the fraction expressed as a number out of 100.
Method 1: The Fraction Method
This is arguably the most intuitive approach, particularly for simpler problems. We begin by expressing the given information as a fraction:
- Part/Whole = 5/15
This fraction represents the ratio of the part to the whole. To convert this fraction to a percentage, we need to find an equivalent fraction with a denominator of 100. We can simplify the fraction first:
- 5/15 = 1/3
Now, we need to convert 1/3 into a fraction with a denominator of 100. To do this, we can set up a proportion:
- 1/3 = x/100
Solving for 'x':
- x = (1 * 100) / 3 = 33.33 (approximately)
Therefore, 5 out of 15 is approximately 33.33%.
Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100. Let's apply this to our problem:
- Part/Whole = 5/15
First, convert the fraction to a decimal by dividing the numerator (5) by the denominator (15):
- 5 ÷ 15 = 0.3333 (approximately)
Now, multiply the decimal by 100 to express it as a percentage:
- 0.3333 * 100 = 33.33% (approximately)
This confirms our result from the fraction method.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process significantly. Simply divide the part by the whole and then multiply by 100. In our case:
- (5 ÷ 15) * 100 = 33.33%
This method is efficient and accurate, especially for more complex calculations.
Understanding Percentage Increase and Decrease
While our example focused on finding a percentage of a whole, percentages are also frequently used to represent changes in values. Let's consider some scenarios:
Percentage Increase:
Imagine you had 10 apples, and you received 5 more. The percentage increase is calculated as follows:
- Find the increase: 5 apples
- Divide the increase by the original amount: 5/10 = 0.5
- Multiply by 100 to express as a percentage: 0.5 * 100 = 50%
Therefore, you experienced a 50% increase in the number of apples.
Percentage Decrease:
Now, let's say you had 15 apples and ate 5. The percentage decrease is:
- Find the decrease: 5 apples
- Divide the decrease by the original amount: 5/15 = 0.3333
- Multiply by 100 to express as a percentage: 0.3333 * 100 = 33.33%
You experienced a 33.33% decrease in the number of apples.
Practical Applications of Percentage Calculations
Percentage calculations are used extensively in various fields:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining sale prices, calculating markups, and analyzing sales data.
- Science: Expressing experimental results, analyzing statistical data, and representing proportions.
- Education: Evaluating test scores, calculating grades, and analyzing student performance.
- Everyday Life: Understanding tips, calculating discounts at the store, and interpreting statistical information in news reports.
Advanced Percentage Problems and Solutions
Let's tackle some more challenging percentage problems to further solidify your understanding.
Problem 1: A store offers a 20% discount on an item originally priced at $50. What is the final price?
- Calculate the discount amount: 20% of $50 = (20/100) * $50 = $10
- Subtract the discount from the original price: $50 - $10 = $40
The final price is $40.
Problem 2: After a 15% increase, the price of a product is $69. What was the original price?
Let 'x' be the original price. The equation is:
- x + 0.15x = $69
- 1.15x = $69
- x = $69 / 1.15 = $60
The original price was $60.
Problem 3: A student scored 80 out of 100 on a test. What is their percentage score?
- (80/100) * 100 = 80%
The student scored 80%.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with different types of percentage problems.
- Understand the concepts: Focus on understanding the underlying principles rather than just memorizing formulas.
- Use different methods: Experiment with various methods (fraction, decimal, calculator) to find the approach that works best for you.
- Break down complex problems: Divide complex problems into smaller, manageable steps.
- Check your answers: Always check your answers to ensure accuracy.
Conclusion
Understanding percentages is a crucial skill that has wide-ranging applications. By mastering the various methods and techniques discussed in this guide, you can confidently tackle percentage problems of varying complexity. Remember to practice regularly and apply your knowledge to real-world scenarios to enhance your understanding and proficiency. Now you not only know that 5 out of 15 is 33.33%, but you possess a comprehensive toolkit to handle a wide array of percentage-related calculations.
Latest Posts
Latest Posts
-
47 Months Is How Many Years
May 15, 2025
-
10 To The Negative Power Of 2
May 15, 2025
-
10 By 10 Room Square Feet
May 15, 2025
-
How Many Yards In A Ton Of Pea Gravel
May 15, 2025
-
What Is The Greatest Common Factor Of 14 And 42
May 15, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 15 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.