5 Out Of 50 As A Percentage
Treneri
May 10, 2025 · 5 min read
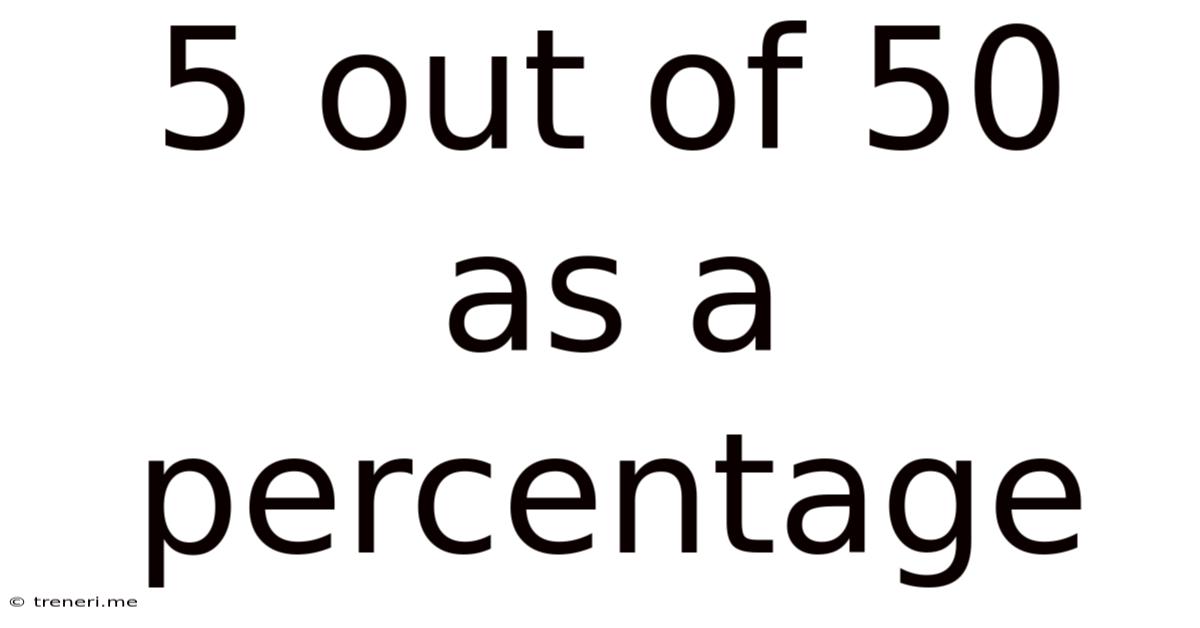
Table of Contents
5 out of 50 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and tips to analyzing data and understanding statistics. Often, we encounter situations where we need to express a ratio as a percentage, and one common scenario involves determining what percentage a smaller number represents of a larger number. This article delves into the specific calculation of 5 out of 50 as a percentage, explaining the process step-by-step, providing alternative methods, and exploring real-world applications of this type of calculation.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the calculation, let's briefly review the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
-
Fraction: A fraction represents a part of a whole using a numerator (top number) and a denominator (bottom number). For example, 5/50 represents 5 parts out of a total of 50 parts.
-
Decimal: A decimal represents a part of a whole using a base-ten system. Decimals are expressed using a decimal point, separating the whole number from the fractional part.
-
Percentage: A percentage represents a part of a whole as a fraction of 100. The symbol "%" is used to denote a percentage.
Calculating 5 out of 50 as a Percentage: The Primary Method
The most straightforward way to calculate 5 out of 50 as a percentage involves these steps:
-
Express as a Fraction: Write the given ratio as a fraction: 5/50
-
Convert to a Decimal: Divide the numerator (5) by the denominator (50): 5 ÷ 50 = 0.1
-
Convert to a Percentage: Multiply the decimal by 100 and add the percent sign (%): 0.1 x 100 = 10%
Therefore, 5 out of 50 is equal to 10%.
Alternative Methods for Calculating Percentages
While the primary method is simple and efficient, there are alternative approaches that can be useful in different contexts.
Method 2: Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage. We can set up a proportion:
5/50 = x/100
Where 'x' represents the unknown percentage. To solve for x, we cross-multiply:
5 * 100 = 50 * x
500 = 50x
x = 500/50
x = 10
Therefore, x = 10%, confirming our previous result.
Method 3: Simplifying the Fraction First
Before converting to a decimal, we can simplify the fraction 5/50 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 5:
5/50 = (5 ÷ 5) / (50 ÷ 5) = 1/10
Now, converting 1/10 to a decimal gives 0.1, and multiplying by 100 gives 10%. This method simplifies the calculation and reduces the risk of errors.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages like 5 out of 50 is crucial in numerous real-world scenarios:
-
Academic Performance: If a student answers 5 out of 50 questions correctly on a test, their score is 10%.
-
Sales and Discounts: A store offering a 10% discount on an item might be offering a discount equivalent to 5 out of 50 of the original price.
-
Financial Calculations: Calculating interest rates, returns on investments, and other financial metrics often involves percentage calculations.
-
Data Analysis: In statistical analysis, percentages are used extensively to represent proportions and trends within datasets. For example, if a survey of 50 people shows 5 prefer a particular brand, that represents 10% market share.
-
Surveys and Polls: Interpreting survey results frequently involves calculating percentages to summarize responses and draw conclusions.
Beyond the Basics: Working with Larger Numbers and More Complex Scenarios
While the example of 5 out of 50 is relatively straightforward, the same principles apply to more complex percentage calculations involving larger numbers. The key is to maintain accuracy in each step:
-
Large Numerators and Denominators: When dealing with larger numbers, using a calculator is highly recommended to ensure accurate decimal conversion.
-
Decimals in the Numerator: If the numerator is a decimal, the process remains the same; simply divide the numerator by the denominator and then multiply by 100.
-
Percentages Greater than 100%: In situations where the numerator is larger than the denominator, the resulting percentage will be greater than 100%. This signifies that the part represents more than the whole, which can occur in certain contexts such as growth or increase.
Practical Tips for Accurate Percentage Calculations
To minimize errors and ensure accurate results when calculating percentages, consider these tips:
-
Use a Calculator: For larger numbers or more complex calculations, use a calculator to avoid manual calculation errors.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
-
Understand the Context: Pay close attention to the context of the problem to interpret the percentage correctly.
-
Practice Regularly: Regular practice is key to mastering percentage calculations.
Conclusion: Mastering Percentage Calculations for Real-World Success
The ability to accurately calculate percentages is a valuable skill that extends far beyond the classroom. From understanding your academic performance to making informed financial decisions and analyzing data effectively, the knowledge of how to calculate percentages, as demonstrated with the example of 5 out of 50, empowers you to navigate various aspects of life with greater confidence and competence. By mastering the fundamental principles outlined in this article, you can confidently tackle a wide range of percentage-related problems and apply this crucial skill to your personal and professional endeavors. Remember to practice regularly, and soon, calculating percentages, no matter the complexity, will become second nature.
Latest Posts
Latest Posts
-
Round 1 316 To The Nearest Hundredth
May 11, 2025
-
What Is The Melt Price Of Gold
May 11, 2025
-
How Big Is 8 Inch Pizza
May 11, 2025
-
1 6 2 In Fraction Form
May 11, 2025
-
3 5 Meters Is How Many Centimeters
May 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.