5 X 1/2 As A Fraction
Treneri
May 11, 2025 · 5 min read
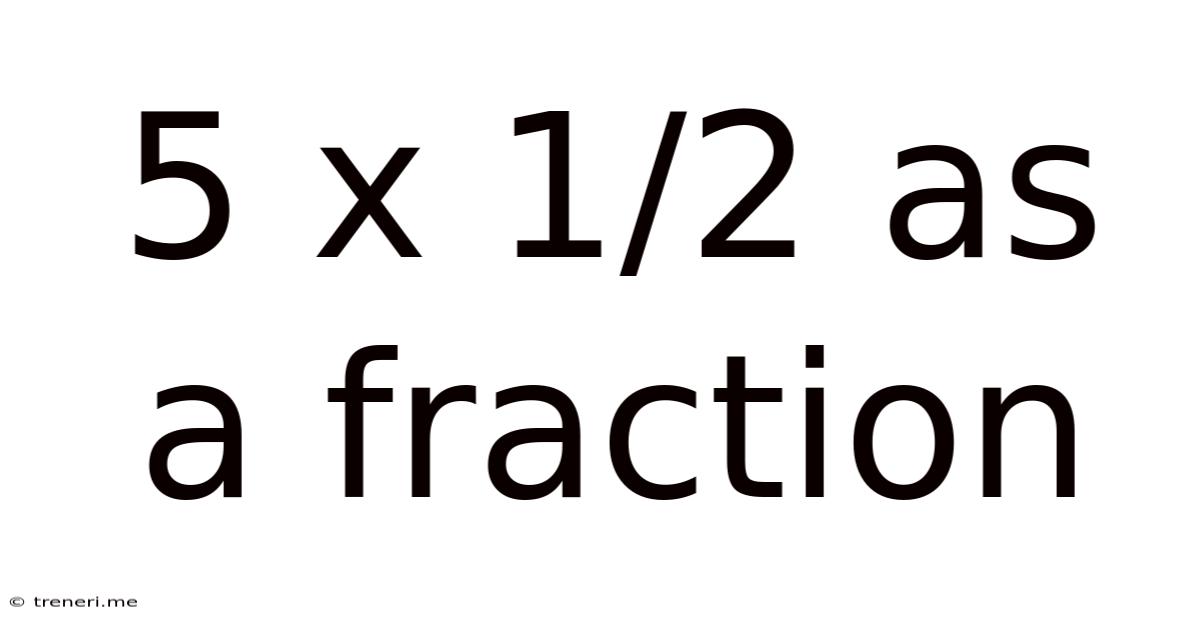
Table of Contents
5 x 1/2 as a Fraction: A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. This comprehensive guide will delve into the seemingly simple problem of calculating 5 x 1/2 as a fraction, exploring the underlying principles, different methods of solving it, and extending the concept to more complex scenarios. We'll also cover practical applications and helpful tips to master fraction multiplication.
Understanding the Basics: Fractions and Multiplication
Before diving into the specific calculation, let's refresh our understanding of fractions and how multiplication applies to them.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For instance, 1/2 represents one out of two equal parts, or one-half.
Multiplying fractions involves multiplying the numerators together to get the new numerator and multiplying the denominators together to get the new denominator. This process is straightforward and easily visualized.
Method 1: Direct Multiplication
The most straightforward way to solve 5 x 1/2 is to treat the whole number 5 as a fraction itself: 5/1. Then, we apply the standard rule for fraction multiplication:
- Numerators: 5 x 1 = 5
- Denominators: 1 x 2 = 2
Therefore, 5 x 1/2 = 5/2.
This fraction, 5/2, is an improper fraction because the numerator is larger than the denominator. Improper fractions are perfectly valid, but they are often converted into mixed numbers for easier understanding and interpretation.
Method 2: Converting to a Mixed Number
An improper fraction like 5/2 can be converted to a mixed number. To do this, we divide the numerator (5) by the denominator (2):
5 ÷ 2 = 2 with a remainder of 1.
This means that 5/2 is equivalent to 2 whole units and 1/2 of a unit. Therefore, the mixed number representation of 5/2 is 2 1/2.
Both 5/2 and 2 1/2 represent the same quantity – they are simply expressed differently. The choice between using an improper fraction or a mixed number often depends on the context of the problem and personal preference.
Method 3: Visual Representation
Visualizing the problem can be particularly helpful, especially for beginners. Imagine five pizzas, each cut into two equal halves. The expression 5 x 1/2 represents taking one-half from each of the five pizzas. Counting the total number of halves, you'll find you have five halves, confirming the result of 5/2 or 2 1/2.
Extending the Concept: More Complex Fraction Multiplication
The principles discussed above can be readily applied to more complex scenarios involving the multiplication of fractions. Let's consider a few examples:
Example 1: 3/4 x 1/2
- Numerators: 3 x 1 = 3
- Denominators: 4 x 2 = 8
Result: 3/8
Example 2: 2 1/3 x 1/2
First, convert the mixed number 2 1/3 to an improper fraction: (2 x 3 + 1)/3 = 7/3
Then, multiply the fractions:
- Numerators: 7 x 1 = 7
- Denominators: 3 x 2 = 6
Result: 7/6 (which can be converted to the mixed number 1 1/6)
Example 3: Multiple Fractions
Multiplying multiple fractions involves extending the same principle: multiply all the numerators together and all the denominators together. For example:
1/2 x 3/4 x 2/5 = (1 x 3 x 2) / (2 x 4 x 5) = 6/40 = 3/20
Always simplify the resulting fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Practical Applications of Fraction Multiplication
Understanding fraction multiplication is essential in numerous real-world situations. Some examples include:
- Cooking and Baking: Scaling recipes up or down requires multiplying fractional amounts of ingredients.
- Construction and Engineering: Calculating dimensions and material quantities often involves fractions.
- Finance: Determining percentages and proportions in financial calculations utilizes fraction multiplication.
- Data Analysis: Interpreting proportions and ratios in data sets frequently requires fraction multiplication.
Simplifying Fractions: A Crucial Step
When working with fractions, it's crucial to simplify your answers to their lowest terms. This means reducing the fraction to its simplest form where the numerator and denominator have no common factors other than 1. For example, 6/12 can be simplified to 1/2 by dividing both the numerator and the denominator by their greatest common divisor, which is 6.
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. Then, divide both the numerator and denominator by the GCD.
Mastering Fraction Multiplication: Tips and Tricks
Here are some helpful tips to improve your proficiency in fraction multiplication:
- Practice Regularly: Consistent practice is key to mastering any mathematical concept. Work through numerous examples, varying the complexity of the fractions involved.
- Visual Aids: Use visual aids like diagrams and illustrations to understand the concept more intuitively, especially when starting out.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps. For example, when dealing with mixed numbers, always convert them to improper fractions first.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Utilize Online Resources: Many online resources provide interactive exercises and tutorials to enhance your understanding of fractions.
Conclusion: 5 x 1/2 and Beyond
This comprehensive guide has explored the calculation of 5 x 1/2 as a fraction, demonstrating various methods and extending the concept to more complex scenarios. Mastering fraction multiplication is a critical skill that underpins many mathematical applications. By understanding the fundamental principles, employing various solution methods, and practicing regularly, you can confidently tackle fraction multiplication problems and apply this knowledge to real-world situations. Remember to always simplify your fractions to their lowest terms for the most accurate and efficient representation. With consistent practice and a thorough understanding of the underlying concepts, you'll find that fractions become less daunting and more manageable.
Latest Posts
Latest Posts
-
Cuanto Falta Para El 11 De Abril
May 12, 2025
-
18 Feet By 18 Feet In Square Meters
May 12, 2025
-
20 Oz Is How Many Milliliters
May 12, 2025
-
Greatest Common Factor Of 10 And 45
May 12, 2025
-
12 By 13 Room In Square Feet
May 12, 2025
Related Post
Thank you for visiting our website which covers about 5 X 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.