54 Divided By 4 With Remainder
Treneri
May 11, 2025 · 5 min read
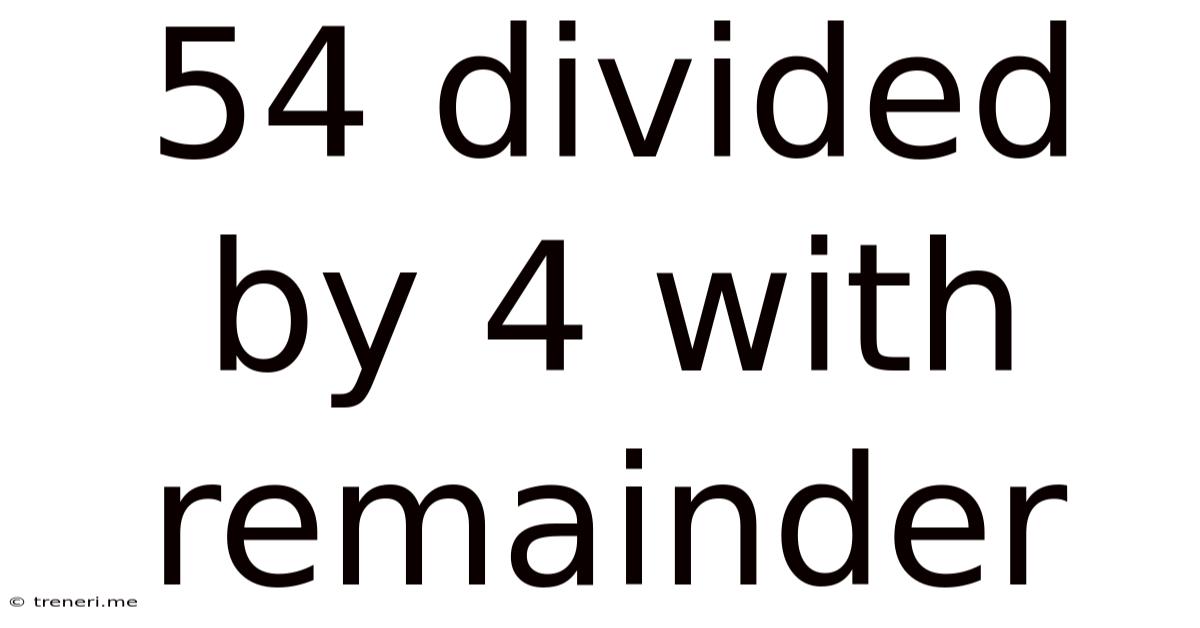
Table of Contents
54 Divided by 4 with Remainder: A Deep Dive into Division with Remainders
Understanding division with remainders is a fundamental concept in mathematics, crucial for various applications from everyday calculations to advanced programming. This article will thoroughly explore the process of dividing 54 by 4, explaining the concept of remainders, different methods to solve the problem, and practical applications of this type of division. We'll also delve into related mathematical concepts to provide a comprehensive understanding.
What is Division with Remainders?
Division with remainders, also known as Euclidean division, is a way of dividing two integers where the result includes both a quotient (the number of times the divisor goes into the dividend) and a remainder (the amount left over). It's represented by the formula:
Dividend = (Divisor × Quotient) + Remainder
In this formula:
- Dividend: The number being divided (in our case, 54).
- Divisor: The number we're dividing by (in our case, 4).
- Quotient: The whole number result of the division.
- Remainder: The amount left over after the division. The remainder is always less than the divisor.
Calculating 54 Divided by 4
Let's now tackle the problem at hand: 54 divided by 4. We can solve this using several methods:
Method 1: Long Division
Long division is a traditional method that provides a step-by-step breakdown of the division process:
-
Set up the problem: Write 54 inside the long division symbol (÷) and 4 outside.
-
Divide the tens: How many times does 4 go into 5? It goes once (1). Write the 1 above the 5.
-
Multiply and subtract: Multiply 1 by 4 (which is 4), and subtract this from 5 (5 - 4 = 1).
-
Bring down the ones: Bring down the 4 from the ones place next to the 1.
-
Divide the ones: How many times does 4 go into 14? It goes 3 times (3). Write the 3 above the 4.
-
Multiply and subtract: Multiply 3 by 4 (which is 12), and subtract this from 14 (14 - 12 = 2).
-
The remainder: The remaining 2 is the remainder.
Therefore, 54 divided by 4 is 13 with a remainder of 2. This can be written as:
54 = (4 × 13) + 2
Method 2: Repeated Subtraction
Repeated subtraction involves repeatedly subtracting the divisor from the dividend until you reach a number smaller than the divisor. The number of times you subtract is the quotient, and the remaining number is the remainder.
- Start with 54.
- Subtract 4: 54 - 4 = 50
- Subtract 4: 50 - 4 = 46
- Subtract 4: 46 - 4 = 42
- Subtract 4: 42 - 4 = 38
- Subtract 4: 38 - 4 = 34
- Subtract 4: 34 - 4 = 30
- Subtract 4: 30 - 4 = 26
- Subtract 4: 26 - 4 = 22
- Subtract 4: 22 - 4 = 18
- Subtract 4: 18 - 4 = 14
- Subtract 4: 14 - 4 = 10
- Subtract 4: 10 - 4 = 6
- Subtract 4: 6 - 4 = 2
We subtracted 4 thirteen times, so the quotient is 13. The remainder is 2.
Method 3: Using Multiplication Tables
This method involves finding the largest multiple of 4 that is less than or equal to 54. We can use multiplication tables to find that 4 x 13 = 52. Then, subtract 52 from 54 to find the remainder: 54 - 52 = 2. The quotient is 13, and the remainder is 2.
Understanding the Remainder
The remainder (2 in this case) signifies the portion of the dividend that cannot be evenly divided by the divisor. It's a crucial part of the result, especially in scenarios where complete division isn't possible or practical. For instance, if you have 54 candies and want to divide them equally among 4 friends, each friend gets 13 candies, and you have 2 candies left over.
Practical Applications of Division with Remainders
Division with remainders has numerous real-world applications across various fields:
-
Sharing items: Distributing items equally among a group of people often results in a remainder (like the candy example).
-
Time calculations: Converting units of time (e.g., minutes into hours) often involves remainders. For instance, 54 minutes is equal to 0 hours and 54 minutes (or 0 hours and 54 minutes).
-
Measurement conversions: Converting between units of measurement (e.g., inches to feet) might leave a remainder.
-
Computer programming: Remainders are used extensively in programming for tasks such as determining even or odd numbers, modular arithmetic, and hash table operations.
-
Scheduling and resource allocation: Planning tasks or allocating resources may involve determining how many complete cycles can be completed and what remains.
Related Mathematical Concepts
Understanding division with remainders enhances your understanding of several related mathematical concepts:
-
Modular arithmetic: Modular arithmetic focuses on remainders after division. It's widely used in cryptography and computer science. In the context of our problem, 54 modulo 4 (written as 54 mod 4) is 2.
-
Factors and multiples: Division with remainders helps determine whether one number is a factor or multiple of another. Since 54 is not divisible by 4, 4 is not a factor of 54.
-
Prime and composite numbers: Understanding remainders aids in identifying prime and composite numbers.
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Algorithms for finding GCD and LCM often involve division with remainders.
Conclusion
Dividing 54 by 4 results in a quotient of 13 and a remainder of 2. This seemingly simple calculation illustrates a fundamental concept in mathematics with wide-ranging applications. Understanding division with remainders is essential for tackling more complex mathematical problems and solving real-world scenarios involving division where a perfect division isn't always possible. By mastering this concept, you'll strengthen your mathematical foundation and enhance your problem-solving abilities. The different methods explained — long division, repeated subtraction, and using multiplication tables — offer various approaches to solve such problems, allowing you to choose the method that best suits your understanding and the context of the problem. Remember, the remainder provides valuable information, often representing the 'leftovers' or the portion that doesn't fit perfectly into the division.
Latest Posts
Latest Posts
-
1 6 1 3 As A Fraction
May 14, 2025
-
How To Calculate Tension In A Cable
May 14, 2025
-
How Many Zeros In 300 Million
May 14, 2025
-
How Do You Figure Out Labor Cost
May 14, 2025
-
How Much Pool Salt To Add
May 14, 2025
Related Post
Thank you for visiting our website which covers about 54 Divided By 4 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.