55 8 As A Mixed Number
Treneri
May 14, 2025 · 5 min read
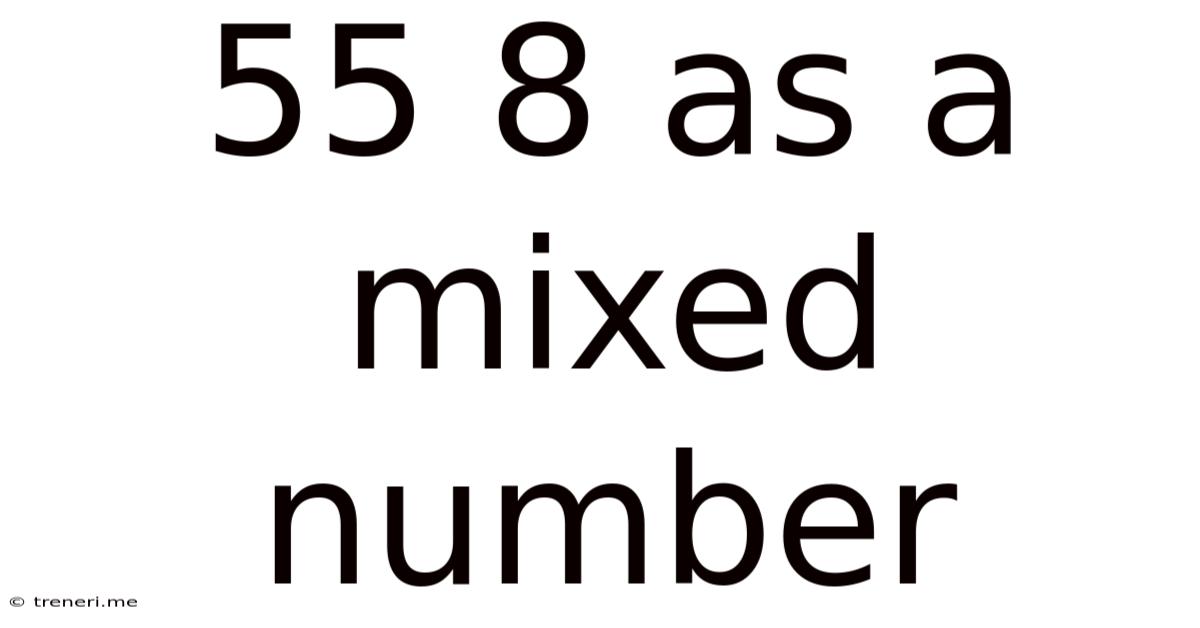
Table of Contents
55/8 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversions is fundamental in mathematics. This comprehensive guide will delve deep into the process of converting the improper fraction 55/8 into a mixed number, exploring the underlying concepts and providing practical examples to solidify your understanding. We'll also cover related topics to ensure a holistic grasp of this crucial mathematical skill.
What is a Mixed Number?
A mixed number is a combination of a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit. Mixed numbers are commonly used to represent quantities that are greater than one but not a whole number.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. The fraction 55/8 is an improper fraction because 55 (the numerator) is larger than 8 (the denominator). Converting an improper fraction to a mixed number involves dividing the numerator by the denominator.
Steps to Convert 55/8 to a Mixed Number:
-
Divide the numerator by the denominator: Divide 55 by 8. 55 ÷ 8 = 6 with a remainder of 7.
-
The quotient becomes the whole number: The quotient (the result of the division) is 6. This will be the whole number part of our mixed number.
-
The remainder becomes the numerator of the fraction: The remainder is 7. This will be the numerator of the fractional part of our mixed number.
-
The denominator stays the same: The denominator remains 8.
-
Combine the whole number and the fraction: Therefore, 55/8 as a mixed number is 6 ⁷/₈.
Understanding the Process: A Deeper Dive
The conversion process essentially represents the division of a larger quantity into smaller, manageable units. In the case of 55/8, we're dividing 55 units into groups of 8. We can form six complete groups of 8 (6 x 8 = 48), leaving 7 units remaining (55 - 48 = 7). These 7 remaining units represent the fraction ⁷/₈.
Visual Representation
Imagine you have 55 identical items. You want to arrange them into groups of 8. You'll be able to make 6 complete groups, with 7 items left over. This visual representation perfectly mirrors the mathematical process of converting 55/8 to the mixed number 6 ⁷/₈.
Practical Applications of Mixed Numbers
Mixed numbers are used extensively in various real-world applications:
-
Measurement: Measuring lengths, weights, or volumes often results in mixed numbers. For example, a board might measure 6 ⁷/₈ inches long.
-
Cooking and Baking: Recipes frequently call for fractional amounts of ingredients, often expressed as mixed numbers for clarity and ease of understanding.
-
Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on the use of fractions, frequently presented as mixed numbers.
-
Everyday Life: Sharing items, dividing resources, or calculating portions often leads to the use of mixed numbers.
Converting Mixed Numbers back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This skill allows for easier calculations when working with mixed numbers in more complex mathematical operations.
Steps to Convert 6 ⁷/₈ back to an Improper Fraction:
-
Multiply the whole number by the denominator: 6 x 8 = 48
-
Add the numerator to the result: 48 + 7 = 55
-
Keep the denominator the same: The denominator remains 8.
-
Combine the numerator and denominator: The resulting improper fraction is 55/8.
Solving Problems Involving Mixed Numbers
Let's illustrate the practical application of converting between improper fractions and mixed numbers with a few examples:
Example 1:
Sarah has 55 cookies. She wants to divide them equally among 8 friends. How many cookies will each friend receive?
- Solution: This problem translates to 55/8. Converting this improper fraction to a mixed number gives us 6 ⁷/₈. Each friend will receive 6 whole cookies, and there will be 7 cookies left over to be shared.
Example 2:
A carpenter needs to cut a piece of wood that is 12 ¾ inches long. Express this measurement as an improper fraction.
- Solution: We convert the mixed number 12 ¾ to an improper fraction: (12 x 4) + 3 = 51. Therefore, the length of the wood is ⁵¹/₄ inches.
Further Exploration: Equivalent Fractions
It's crucial to understand the concept of equivalent fractions. These are fractions that represent the same value even though they have different numerators and denominators. For example, ⁴/₈, ⁶/₁₂, and ¹²/₂₄ are all equivalent fractions, all equal to ½. Understanding equivalent fractions helps in simplifying fractions and performing calculations more efficiently. You can find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number.
The Importance of Mastering Fractions
Mastering the conversion between improper fractions and mixed numbers, along with a solid understanding of equivalent fractions, is paramount for success in mathematics and its many applications. This skill provides a foundation for more advanced mathematical concepts and problem-solving. Consistent practice and a clear understanding of the underlying principles are key to achieving proficiency in this area.
Common Mistakes to Avoid
-
Incorrect division: Ensure you accurately divide the numerator by the denominator when converting to a mixed number.
-
Forgetting the remainder: The remainder is crucial; it forms the numerator of the fractional part of the mixed number.
-
Incorrect multiplication/addition: When converting from a mixed number back to an improper fraction, ensure accurate multiplication and addition steps.
-
Ignoring the denominator: The denominator remains constant throughout the conversion process.
Conclusion
Converting 55/8 to a mixed number, which results in 6 ⁷/₈, is a straightforward process that underpins many mathematical applications. A thorough understanding of this conversion, along with the related concepts of proper and improper fractions, equivalent fractions, and the reverse conversion process, equips you with a valuable skillset for various mathematical challenges. Practice is key to mastering these concepts and developing confidence in working with fractions. Through consistent practice and a clear understanding of the underlying principles, you can become proficient in handling fractions and their various forms. Remember to always double-check your calculations to avoid common errors. The ability to seamlessly convert between improper fractions and mixed numbers is a fundamental skill that will benefit you in numerous contexts.
Latest Posts
Latest Posts
-
Calculate How Much Heat Will Be Released Or Absorbed
May 15, 2025
-
What Is The Least Common Multiple Of 24 And 9
May 15, 2025
-
Cuanto Es 54 Grados Fahrenheit En Grados Celsius
May 15, 2025
-
Round 149 To The Nearest Hundred
May 15, 2025
-
Round 156 To The Nearest Hundred
May 15, 2025
Related Post
Thank you for visiting our website which covers about 55 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.