6.072 X 10 To The 3rd Power
Treneri
May 12, 2025 · 6 min read
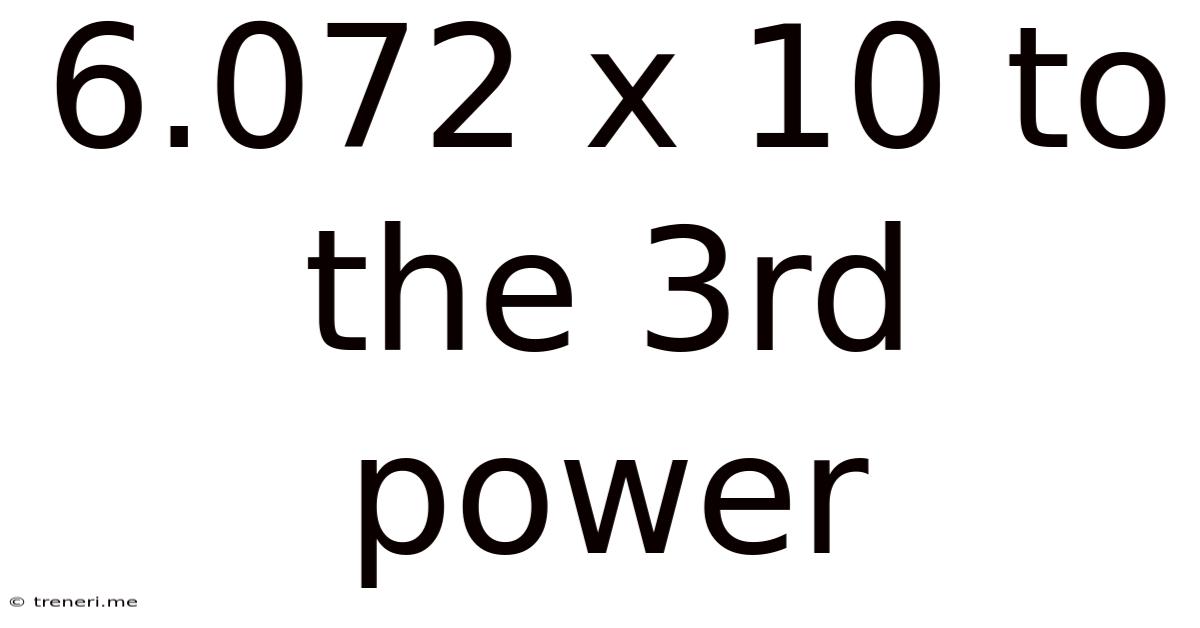
Table of Contents
Decoding 6.072 x 10³: A Deep Dive into Scientific Notation and its Applications
Scientific notation is a powerful tool used to represent extremely large or small numbers concisely. Understanding this notation is crucial in various fields, from engineering and physics to finance and computer science. This article will comprehensively explore the meaning and applications of 6.072 x 10³, providing a detailed explanation and numerous examples to solidify your understanding.
Understanding Scientific Notation
Scientific notation expresses numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer representing the power of 10. This format significantly simplifies the handling of very large or small numbers, making calculations and comparisons much easier.
The exponent 'b' indicates how many places the decimal point needs to be moved to obtain the standard form of the number. A positive exponent means moving the decimal point to the right (making the number larger), while a negative exponent means moving it to the left (making the number smaller).
Breaking Down 6.072 x 10³
Let's dissect the given number: 6.072 x 10³.
- 6.072: This is our 'a' value, a number between 1 and 10.
- 10³: This is our 'b' value, representing 10 raised to the power of 3. 10³ is equal to 10 x 10 x 10 = 1000.
Therefore, 6.072 x 10³ is equivalent to 6.072 multiplied by 1000. Performing this multiplication, we arrive at the standard form: 6072.
Applications of Scientific Notation
The utility of scientific notation extends across numerous disciplines. Let's delve into some key areas:
1. Physics and Engineering
In physics and engineering, dealing with extremely large or small quantities is commonplace. For instance:
-
Avogadro's Number: This fundamental constant in chemistry represents the number of constituent particles (atoms, molecules, ions, etc.) in one mole of a substance. It's approximately 6.022 x 10<sup>23</sup>, a number far too cumbersome to write in standard form. Scientific notation simplifies this significantly.
-
Distances in Astronomy: Measuring distances between celestial bodies often involves incredibly large numbers. The distance to the nearest star (Proxima Centauri) is about 4.243 x 10<sup>13</sup> kilometers. Scientific notation makes these vast distances manageable.
-
Microscopic Measurements: In nanotechnology and material science, measurements often involve extremely small scales. The size of a typical atom might be expressed as 1 x 10<sup>-10</sup> meters, again highlighting the efficiency of scientific notation.
2. Computer Science
Computer science relies heavily on binary systems and large data sets. Scientific notation is instrumental in:
-
Memory Representation: Computer memory is often measured in gigabytes (GB) or terabytes (TB), which are expressed using powers of 10 (1 GB = 10<sup>9</sup> bytes, 1 TB = 10<sup>12</sup> bytes).
-
Data Storage and Transfer: Large datasets, like those used in machine learning and big data analytics, are often described using scientific notation to convey their immense size efficiently.
-
Floating-Point Numbers: Computers use floating-point representation to store real numbers, which often employs a format similar to scientific notation to balance precision and range.
3. Finance
In finance, scientific notation proves useful when dealing with:
-
National Debts and Budgets: National debts and government budgets often involve numbers in the trillions, easily represented using scientific notation for clarity and comparisons.
-
Global Markets: Tracking global market indices, trading volumes, and investment portfolios frequently necessitates handling extremely large numbers, making scientific notation essential for efficient data management and analysis.
-
Financial Modeling: Complex financial models often involve calculations with vast quantities of data; scientific notation greatly simplifies these calculations and improves computational efficiency.
4. Chemistry
In chemistry, dealing with extremely small amounts of substances is commonplace. This is where scientific notation shines:
-
Molar Mass Calculations: Calculations involving molar masses of elements and compounds frequently lead to very small numbers, readily expressed using scientific notation.
-
Chemical Reaction Stoichiometry: In chemical reaction calculations, the quantities involved can vary enormously, making scientific notation an indispensable tool.
-
Concentration Units: Concentration units such as molarity (moles per liter) often result in values best expressed using scientific notation, particularly when dealing with dilute solutions.
5. Biology
Biology also utilizes scientific notation to represent large quantities and tiny measurements:
-
Population Sizes: Tracking population sizes of various species, especially microorganisms, often involves extremely large numbers, making scientific notation necessary for clear and concise representation.
-
Microbial Growth: Understanding microbial growth dynamics and calculating population growth rates involves dealing with enormous numbers of organisms, where scientific notation provides a practical solution.
-
Genetic Sequencing: The analysis of genetic sequences and DNA involves sequences of millions or billions of base pairs, for which scientific notation is perfectly suited.
Working with 6.072 x 10³: Examples and Calculations
Let's explore some practical examples using 6.072 x 10³ (or 6072):
Example 1: Addition
Add 6072 to 1500:
6072 + 1500 = 7572
Example 2: Subtraction
Subtract 2350 from 6072:
6072 - 2350 = 3722
Example 3: Multiplication
Multiply 6072 by 5:
6072 x 5 = 30360
Example 4: Division
Divide 6072 by 12:
6072 / 12 = 506
Example 5: Real-world application (Area Calculation)
Imagine a rectangular field with dimensions 6072 meters by 200 meters. To find the area, we multiply the length and width:
Area = 6072 m x 200 m = 1,214,400 square meters
Converting to and from Scientific Notation
Converting between standard form and scientific notation is a vital skill. Here's how:
Converting from Standard Form to Scientific Notation:
- Locate the decimal point: In 6072, the decimal point is implicitly at the end (6072.).
- Move the decimal point: Move the decimal point to the left until you have a number between 1 and 10. In this case, we move it three places to the left, resulting in 6.072.
- Determine the exponent: The number of places you moved the decimal point becomes the exponent. Since we moved it three places to the left, the exponent is 3.
- Write in scientific notation: The number in scientific notation is 6.072 x 10³.
Converting from Scientific Notation to Standard Form:
- Identify the exponent: In 6.072 x 10³, the exponent is 3.
- Move the decimal point: Move the decimal point to the right the number of places indicated by the exponent. Since the exponent is 3, we move the decimal point three places to the right.
- Write in standard form: This gives us 6072.
Conclusion
Scientific notation is a fundamental tool for representing and manipulating very large or very small numbers concisely and efficiently. Its applications span numerous scientific, technological, and financial fields, simplifying calculations and enhancing understanding. A thorough grasp of scientific notation, as exemplified by our exploration of 6.072 x 10³, is essential for success in various disciplines. By mastering this notation, you equip yourself with a powerful tool for tackling complex numerical challenges with clarity and ease.
Latest Posts
Latest Posts
-
Cuanta Leche Materna Debe Tomar Un Recien Nacido
May 12, 2025
-
60 Days From June 8 2024
May 12, 2025
-
Cuanto Es 500 Ml De Agua
May 12, 2025
-
Buy 2 Get 1 Free Discount Percentage
May 12, 2025
-
How To Calculate The Change In Kinetic Energy
May 12, 2025
Related Post
Thank you for visiting our website which covers about 6.072 X 10 To The 3rd Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.