6/7 Divided By 1/6 As A Fraction
Treneri
May 11, 2025 · 5 min read
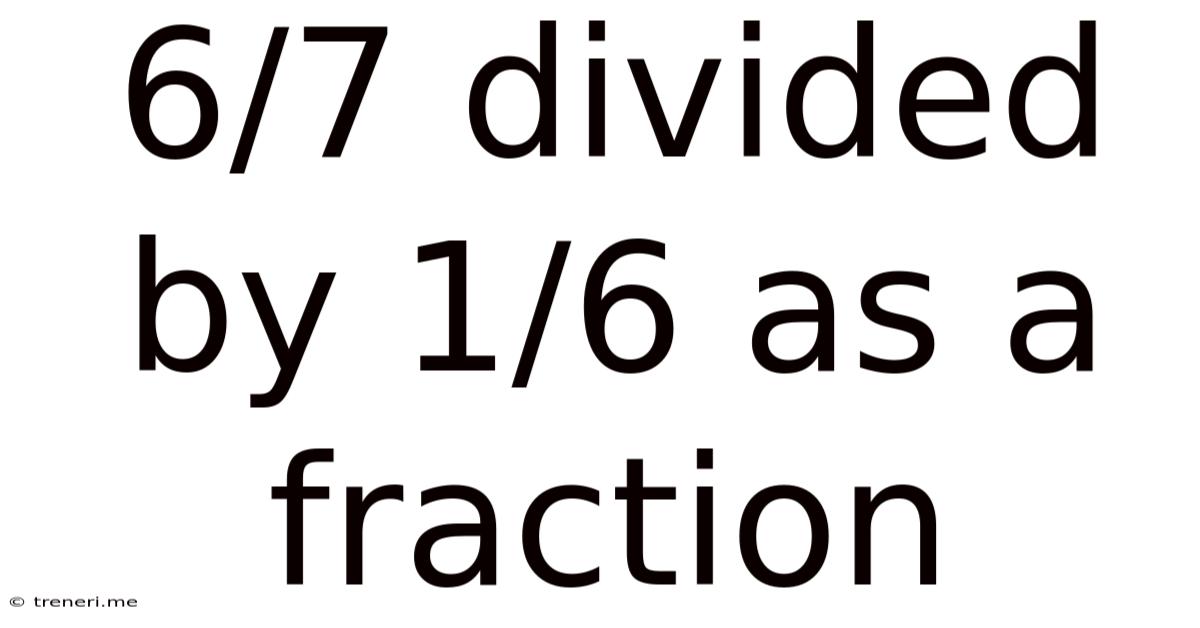
Table of Contents
6/7 Divided by 1/6 as a Fraction: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will thoroughly explain how to solve 6/7 divided by 1/6, not just providing the answer, but also delving into the underlying principles and offering various approaches to tackle similar problems. We'll explore the concept of reciprocal fractions, the importance of understanding division as the inverse of multiplication, and provide practical examples to solidify your understanding. By the end, you'll be confident in solving fraction division problems independently.
Understanding Fraction Division
Before tackling our specific problem (6/7 ÷ 1/6), let's refresh our understanding of fraction division. The core principle is that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/6 is 6/1 (or simply 6).
This means that the equation a/b ÷ c/d is equivalent to a/b × d/c. This is a crucial concept that forms the basis for solving any fraction division problem.
Step-by-Step Solution: 6/7 ÷ 1/6
Now, let's solve 6/7 divided by 1/6 step-by-step:
-
Identify the reciprocal: The reciprocal of 1/6 is 6/1 (or 6).
-
Rewrite the division as multiplication: Replace the division sign (÷) with a multiplication sign (×) and use the reciprocal of the second fraction. Our equation now becomes: 6/7 × 6/1
-
Multiply the numerators: Multiply the numerators (the top numbers) together: 6 × 6 = 36
-
Multiply the denominators: Multiply the denominators (the bottom numbers) together: 7 × 1 = 7
-
Simplify the resulting fraction: Our resulting fraction is 36/7. This is an improper fraction (where the numerator is larger than the denominator). We can convert this to a mixed number if desired.
-
Convert to a mixed number (optional): To convert 36/7 to a mixed number, we divide the numerator (36) by the denominator (7). 36 ÷ 7 = 5 with a remainder of 1. This means 36/7 is equal to 5 1/7.
Therefore, 6/7 ÷ 1/6 = 36/7 = 5 1/7
Alternative Methods and Visualizations
While the method above is the most common and efficient, let's explore alternative ways to visualize and solve this problem:
Using a Visual Model (Area Model)
Imagine a rectangle representing the fraction 6/7. We want to divide this rectangle into pieces representing 1/6. This visual representation can help solidify the understanding of the division process. However, for complex fractions, the visual model becomes less practical.
Breaking Down the Problem
We can also break down the problem into smaller, manageable steps. Think of it as asking, "How many 1/6s are there in 6/7?" This approach emphasizes the meaning of division. The solution, 36/7 or 5 1/7, represents the number of 1/6 fractions that fit within 6/7.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving textbook problems; it has many real-world applications:
-
Cooking and Baking: Many recipes require precise measurements. If a recipe calls for 1/3 of a cup of flour but you only want to make 1/2 of the recipe, you need to divide 1/3 by 2 (or multiply by 1/2), requiring fraction division skills.
-
Sewing and Crafting: Creating projects often involves precise measurements of fabric, yarn, or other materials. Dividing lengths or quantities of materials frequently involves working with fractions.
-
Construction and Engineering: Many construction projects require precise calculations involving fractions of inches or feet. Accurate measurements and calculations are essential for the structural integrity and functionality of any construction.
-
Data Analysis: When analyzing data, you often encounter fractions and need to perform calculations like finding the average of fractional values.
Troubleshooting Common Mistakes
When working with fraction division, several common mistakes can arise:
-
Forgetting the reciprocal: This is the most frequent error. Remember that division by a fraction is equivalent to multiplication by its reciprocal.
-
Incorrectly multiplying numerators and denominators: Double-check your multiplication to ensure accuracy.
-
Failing to simplify the fraction: Always simplify the final answer to its lowest terms. An unsimplified fraction is considered an incomplete answer.
-
Confusing division and multiplication: Make sure you understand the difference between multiplying and dividing fractions.
Expanding Your Knowledge: More Complex Fraction Division
The principles discussed here apply to more complex fraction division problems as well. For instance, if you encountered a problem like (3/5 ÷ 2/7) × (1/4 ÷ 3/8), you would follow the same steps:
- Convert all divisions to multiplication using reciprocals.
- Multiply the numerators and denominators separately.
- Simplify the resulting fraction.
Remember to take it one step at a time and apply the reciprocal rule consistently.
Conclusion: Mastering Fraction Division
Mastering fraction division is a valuable skill with wide-ranging applications. By understanding the concept of reciprocals, meticulously following the steps, and practicing regularly, you'll develop confidence and accuracy in solving fraction division problems of any complexity. Remember to check your work for accuracy and simplify your answers. Through practice and consistent application of these techniques, you will become proficient in this essential mathematical skill. Don't be afraid to work through many examples to reinforce your understanding and build your problem-solving skills. The more you practice, the easier it will become!
Latest Posts
Latest Posts
-
What Size Trash Bag For 27 Quart Can
May 12, 2025
-
Kernels In A Bushel Of Corn
May 12, 2025
-
285 Rounded To The Nearest Hundred
May 12, 2025
-
Cuanto Falta Para El 5 De Febrero
May 12, 2025
-
How Much Is 130 Minutes In Hours
May 12, 2025
Related Post
Thank you for visiting our website which covers about 6/7 Divided By 1/6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.