6 Is What Percent Of 21
Treneri
May 13, 2025 · 5 min read
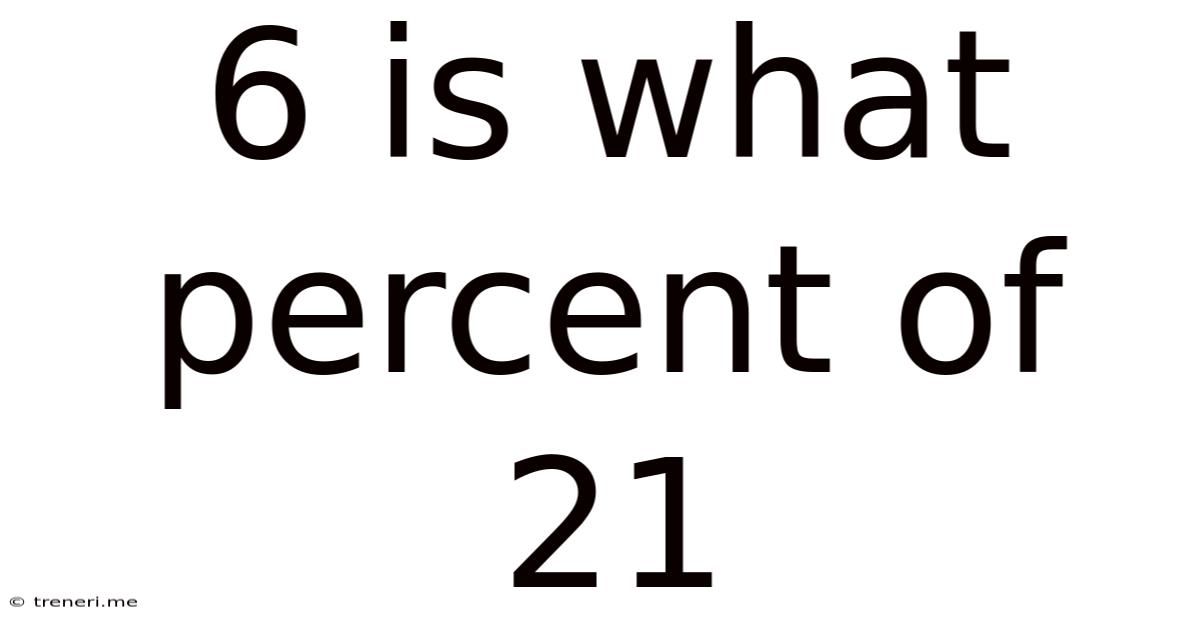
Table of Contents
6 is What Percent of 21? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "6 is what percent of 21?", opens the door to a world of practical applications for understanding percentages. Percentages are fundamental to everyday life, from calculating discounts and taxes to understanding statistics and financial reports. Mastering percentage calculations empowers you to make informed decisions and confidently navigate various numerical scenarios. This comprehensive guide will not only answer the initial question but also equip you with the knowledge and skills to tackle similar problems with ease.
Understanding Percentages: The Basics
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ( per cent). For example, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
This fundamental concept is crucial because it provides a standardized way to compare different proportions. Whether we're discussing the success rate of a marketing campaign (e.g., 15% conversion rate), the interest rate on a loan (e.g., 5% annual interest), or the discount on a sale item (e.g., 30% off), percentages provide a common ground for understanding and comparing these disparate situations.
Calculating Percentages: The Formula
The core formula for calculating percentages is remarkably straightforward:
(Part / Whole) * 100% = Percentage
Let's break down each component:
-
Part: This represents the specific portion you're interested in expressing as a percentage. In our initial question, "6 is what percent of 21?", the part is 6.
-
Whole: This represents the total amount or the entire quantity. In our example, the whole is 21.
-
Percentage: This is the result you're calculating – the numerical representation of the part as a percentage of the whole.
Solving "6 is What Percent of 21?"
Now, let's apply the formula to our original question:
-
Identify the Part and the Whole: Part = 6, Whole = 21
-
Apply the Formula: (6 / 21) * 100% = Percentage
-
Calculate: 6 divided by 21 is approximately 0.2857.
-
Multiply by 100%: 0.2857 * 100% = 28.57%
Therefore, 6 is approximately 28.57% of 21.
Alternative Methods and Approaches
While the primary formula provides a clear and concise method, understanding alternative approaches can enhance your problem-solving skills and provide flexibility in different contexts.
Method 2: Using Proportions
Percentages can be elegantly solved using proportions. We can set up a proportion to represent the relationship between the part, the whole, and the unknown percentage:
6/21 = x/100
Solving for 'x' will yield the percentage. Cross-multiplying gives us:
21x = 600
x = 600/21 ≈ 28.57
This method demonstrates the equivalence between fractions and percentages, strengthening your understanding of the underlying mathematical principles.
Method 3: Decimal Conversion
Another approach involves converting the fraction to a decimal first, then multiplying by 100%:
-
Convert the fraction 6/21 to a decimal: 6 ÷ 21 ≈ 0.2857
-
Multiply the decimal by 100%: 0.2857 * 100% = 28.57%
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a multitude of real-world scenarios. Here are a few examples:
-
Financial Calculations: Determining interest earned on savings accounts, calculating discounts on purchases, understanding loan interest rates, and analyzing investment returns all rely heavily on percentage calculations. Understanding these percentages helps in making informed financial decisions.
-
Statistical Analysis: Percentages are essential for interpreting statistical data. For instance, understanding the percentage of respondents who answered "yes" to a survey question, calculating the success rate of a marketing campaign, or analyzing the percentage change in sales figures over time.
-
Scientific Applications: Percentages are used widely in scientific fields such as chemistry (concentration of solutions), biology (population growth rates), and physics (efficiency of energy conversion). Accuracy in percentage calculations is crucial for obtaining reliable results in these fields.
-
Everyday Life: From calculating tips in restaurants to figuring out sale prices in stores and understanding tax rates, percentage calculations are embedded in our daily routines. Mastering percentage calculation empowers you to make quick, accurate assessments and save time and money.
Advanced Percentage Problems and Strategies
As your understanding of percentages grows, you'll encounter more complex problems. Here are some advanced concepts to explore:
-
Percentage Increase and Decrease: Calculating the percentage change between two values requires an understanding of the difference between the initial and final values, expressed as a percentage of the initial value.
-
Percentage Points vs. Percentage Change: It's important to differentiate between a percentage point change and a percentage change. A percentage point change is the simple difference between two percentages, while a percentage change represents the relative change expressed as a percentage of the initial value.
-
Compound Interest: Compound interest involves calculating interest not only on the principal amount but also on the accumulated interest over time. This introduces exponential growth, requiring a different approach than simple percentage calculations.
Conclusion: Mastering Percentages for a Brighter Future
This in-depth exploration of percentage calculations, specifically addressing the question "6 is what percent of 21?", has provided you with a strong foundation in this essential mathematical concept. By understanding the underlying formulas, applying various calculation methods, and recognizing the wide-ranging applications of percentages, you're now equipped to confidently tackle a variety of numerical problems. The skills you've acquired will prove invaluable in navigating the complexities of daily life, making informed decisions in various domains, and achieving success in your personal and professional endeavors. Remember that consistent practice is key to mastering any mathematical skill, so continue exploring different problems and challenging yourself with increasingly complex scenarios. With dedication and perseverance, your proficiency in percentage calculations will only improve over time, empowering you to confidently tackle any numerical challenge that comes your way.
Latest Posts
Latest Posts
-
What Is The Gcf Of 2 And 8
May 13, 2025
-
Round 42 To The Nearest Ten
May 13, 2025
-
Poissons Ratio Formula In Terms Of Youngs Modulus
May 13, 2025
-
Cuantas Calorias Debo Consumir Al Dia
May 13, 2025
-
How Old Is 1982 To 2023
May 13, 2025
Related Post
Thank you for visiting our website which covers about 6 Is What Percent Of 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.