6 Is What Percent Of 32
Treneri
May 13, 2025 · 4 min read
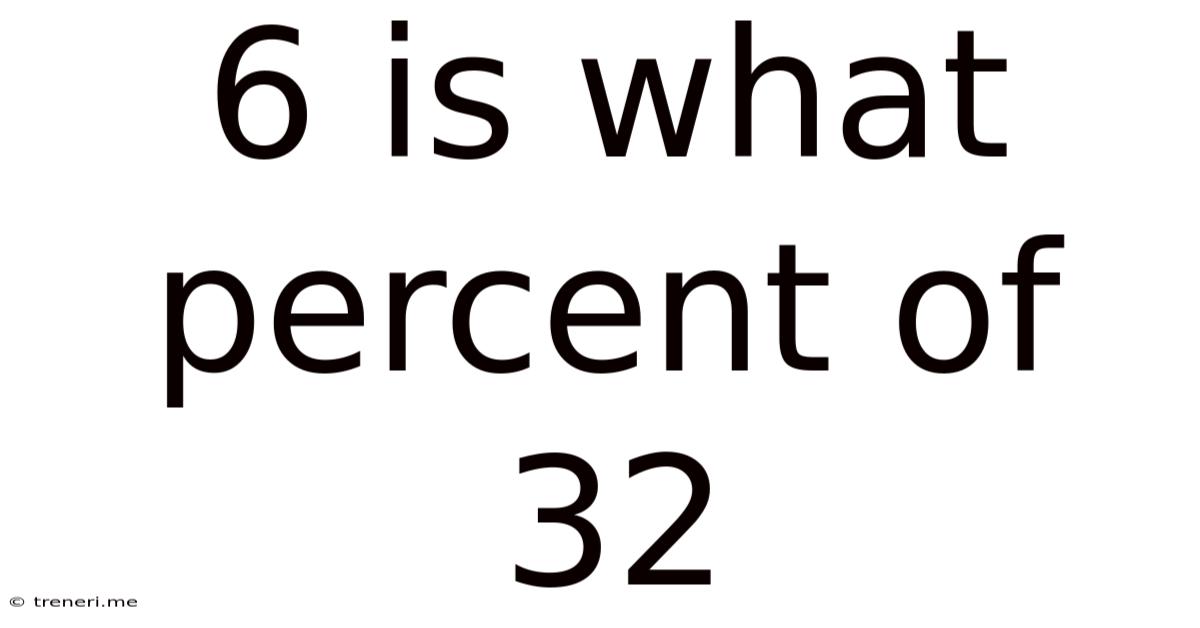
Table of Contents
6 is What Percent of 32? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and sales tax to analyzing data and understanding financial reports. This article will comprehensively explore how to determine what percent 6 is of 32, providing multiple approaches and explaining the underlying concepts. We'll go beyond a simple answer, diving into the methods, real-world applications, and even tackling some related percentage problems to solidify your understanding.
Understanding Percentages: The Basics
Before we delve into the specific problem of "6 is what percent of 32?", let's review the fundamentals of percentages. A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100". For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Method 1: Using the Percentage Formula
The most straightforward approach to solving "6 is what percent of 32?" is by using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 6
- Whole: 32
Substituting these values into the formula, we get:
(6 / 32) x 100% = 0.1875 x 100% = 18.75%
Therefore, 6 is 18.75% of 32.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation that states that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
6/32 = x/100
To solve for x, we cross-multiply:
6 * 100 = 32 * x
600 = 32x
x = 600 / 32
x = 18.75
Therefore, x = 18.75%, confirming our previous result.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
First, we express the relationship as a fraction: 6/32
Next, we divide 6 by 32:
6 ÷ 32 = 0.1875
Finally, we multiply the decimal by 100% to express it as a percentage:
0.1875 x 100% = 18.75%
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in many everyday scenarios. Here are some examples:
1. Calculating Discounts:
Imagine a $32 item is on sale for $6 off. To determine the discount percentage, we use the same formula:
(Discount / Original Price) x 100% = Discount Percentage
($6 / $32) x 100% = 18.75%
The item is on sale for an 18.75% discount.
2. Determining Sales Tax:
If a $32 purchase incurs a 6% sales tax, the tax amount is calculated as:
(Sales Tax Percentage / 100) x Purchase Price = Sales Tax Amount
(6/100) x $32 = $1.92
The sales tax would be $1.92.
3. Analyzing Test Scores:
If you scored 6 points out of a possible 32 points on a quiz, your percentage score would be 18.75%, calculated as demonstrated above.
4. Understanding Financial Reports:
Percentage changes in stock prices, profit margins, and other financial metrics are frequently used to analyze business performance. Understanding percentage calculations is essential for interpreting these reports effectively.
5. Calculating Tip Amounts:
Many people calculate tips as a percentage of the bill. For example, a 15% tip on a $32 meal would be (15/100) x $32 = $4.80
Addressing Potential Errors and Misconceptions
When dealing with percentages, several common errors can occur. Here are a few to watch out for:
-
Incorrect Formula Application: Ensure you are using the correct formula and substituting the values correctly. Double-checking your work is crucial.
-
Decimal Errors: Be careful when working with decimals, especially during conversions. Round to the appropriate number of decimal places depending on the context of the problem.
-
Confusing Part and Whole: Make sure you clearly identify the "part" and the "whole" in the problem. The "whole" is the total amount or the original value, while the "part" is the portion you're comparing to the whole.
Expanding Your Understanding: Further Percentage Problems
Let's practice with a few more percentage problems to solidify your understanding:
Problem 1: What is 25% of 80?
Using the formula: (25/100) x 80 = 20
Problem 2: 15 is what percent of 60?
Using the formula: (15/60) x 100% = 25%
Problem 3: 20 is 40% of what number?
Let 'x' represent the unknown number. We can set up the equation:
0.40x = 20
x = 20 / 0.40
x = 50
Conclusion: Mastering Percentage Calculations
Calculating percentages is a vital skill applicable across numerous fields. By understanding the different methods – using the percentage formula, setting up proportions, or converting to decimals – you can accurately determine percentages in various contexts. Remember to practice consistently and pay attention to detail to avoid common errors. This comprehensive guide has provided you with the tools and understanding necessary to confidently tackle percentage calculations in your daily life, professional endeavors, and academic pursuits. Mastering this fundamental skill opens up a world of possibilities in understanding data, making informed decisions, and navigating the numerical complexities of our modern world.
Latest Posts
Latest Posts
-
How Many Cm Is 7 1 4 Hat Size
May 13, 2025
-
How Much Is 35 Km In Miles
May 13, 2025
-
How Many Cows Per Acre In Florida
May 13, 2025
-
How Many Cups In 160 Ml
May 13, 2025
-
What Is The Greatest Common Factor Of 64 And 24
May 13, 2025
Related Post
Thank you for visiting our website which covers about 6 Is What Percent Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.