6 Is What Percent Of 80
Treneri
May 08, 2025 · 4 min read
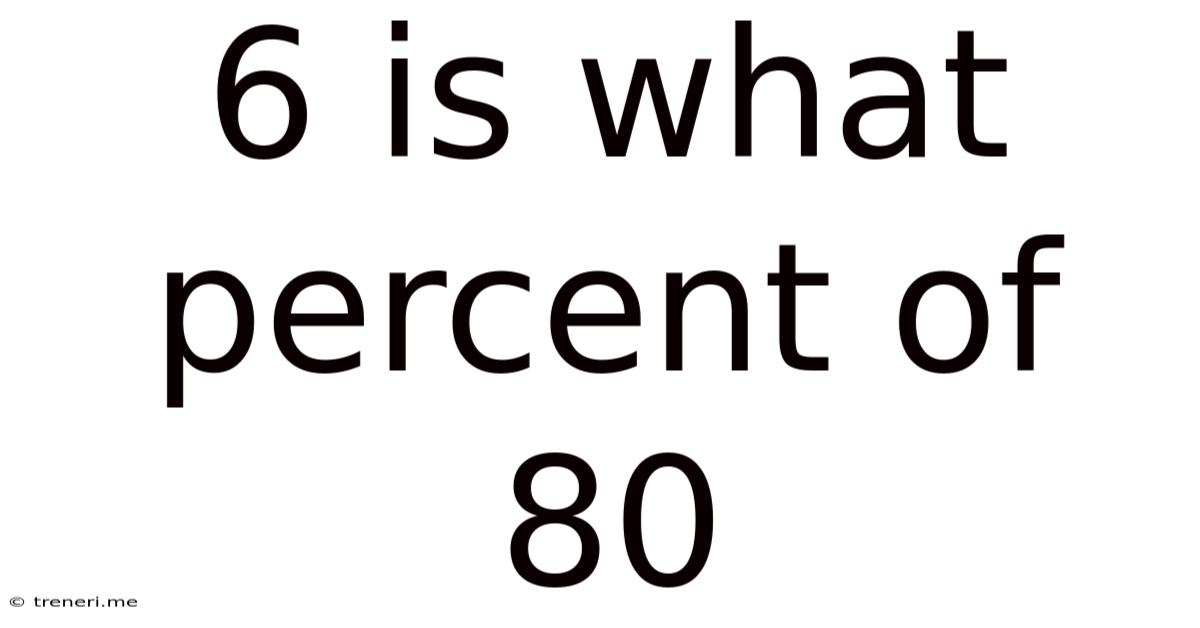
Table of Contents
6 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve deep into how to calculate "6 is what percent of 80?", explaining the process step-by-step, providing alternative methods, and exploring real-world applications. We'll also touch upon advanced concepts and strategies to master percentage calculations.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's establish a strong foundation in percentage calculations. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100."
For example, 50% means 50 out of 100, which can also be expressed as the fraction 50/100 or the decimal 0.5.
The basic formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
Where:
- Part: Represents the portion you're interested in.
- Whole: Represents the total amount.
Calculating "6 is What Percent of 80?"
Now, let's apply this knowledge to solve the problem: "6 is what percent of 80?"
In this scenario:
- Part = 6
- Whole = 80
Using the formula:
(6 / 80) x 100% = Percentage
-
Divide the Part by the Whole: 6 / 80 = 0.075
-
Multiply by 100%: 0.075 x 100% = 7.5%
Therefore, 6 is 7.5% of 80.
Alternative Methods for Percentage Calculation
While the above method is straightforward, there are other ways to approach this problem, particularly useful for mental calculations or when working with less straightforward numbers.
Method 2: Using Proportions
Proportions offer a visual and intuitive approach to percentage problems. We can set up a proportion:
6/80 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x':
Cross-multiply: 6 * 100 = 80 * x
600 = 80x
Divide both sides by 80: x = 600 / 80 = 7.5
Therefore, x = 7.5%, confirming our previous result.
Method 3: Working with Decimals
You can also solve this problem by converting the fraction to a decimal and then multiplying by 100:
6/80 = 0.075
0.075 * 100 = 7.5%
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in many everyday situations:
-
Discounts: Calculating the final price of an item after a percentage discount. For instance, a 20% discount on a $100 item would result in a $20 discount ($100 * 0.20 = $20), leaving a final price of $80.
-
Taxes: Determining the total cost of an item after adding sales tax. A 6% sales tax on a $50 item adds $3 ($50 * 0.06 = $3), resulting in a total cost of $53.
-
Tips: Calculating the appropriate tip amount in a restaurant. A 15% tip on a $75 bill would be $11.25 ($75 * 0.15 = $11.25).
-
Interest Rates: Understanding interest earned on savings accounts or interest paid on loans. A 5% interest rate on a $1000 investment means you'll earn $50 in interest ($1000 * 0.05 = $50) in a year.
-
Grade Calculations: Determining your final grade in a class based on individual assignment scores and weights.
Advanced Percentage Concepts and Problem Solving
While the basic formula covers most scenarios, understanding more advanced concepts can enhance your problem-solving skills:
-
Percentage Increase/Decrease: Calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] x 100%. For example, if a price increases from $50 to $60, the percentage increase is [(60-50)/50] x 100% = 20%.
-
Compound Interest: Calculating interest earned on both the principal amount and accumulated interest. This is more complex and usually involves exponential growth formulas.
-
Percentage Points vs. Percentages: A crucial distinction: Percentage points represent the absolute difference between two percentages, while percentages refer to the relative change. For example, if interest rates increase from 2% to 5%, this is a 3 percentage point increase, but a 150% relative increase ((5-2)/2 * 100%).
Improving Your Percentage Calculation Skills
Mastering percentage calculations requires practice and understanding. Here are some tips:
-
Practice Regularly: Solve various percentage problems from different sources.
-
Use Multiple Methods: Experiment with different approaches (like the ones described above) to solidify your understanding and find the method that works best for you.
-
Visual Aids: Use diagrams or charts to visualize the problem.
-
Check Your Work: Always verify your calculations to avoid errors. Use a calculator to double-check your manual calculations, especially for complex problems.
Conclusion: Mastering the Power of Percentages
Understanding how to calculate percentages is a critical life skill with a wide range of applications. By mastering the fundamental formula and exploring alternative methods, you'll be well-equipped to handle various percentage-related problems confidently and efficiently. Remember to practice regularly and delve into advanced concepts to further enhance your proficiency. The ability to quickly and accurately calculate percentages is a valuable asset in both personal and professional contexts. So, next time you encounter a percentage problem, remember the steps outlined in this comprehensive guide and solve it with confidence!
Latest Posts
Latest Posts
-
How Many Hours Is 38 Days
May 11, 2025
-
How Big Is 7 Inch Pizza
May 11, 2025
-
How To Find Height Of Trapezoid Without Area
May 11, 2025
-
Cuanto Te Crece El Pelo En 3 Dias
May 11, 2025
-
Calculate The Change In Kinetic Energy
May 11, 2025
Related Post
Thank you for visiting our website which covers about 6 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.