60 Is 2 Percent Of What Number
Treneri
May 12, 2025 · 5 min read
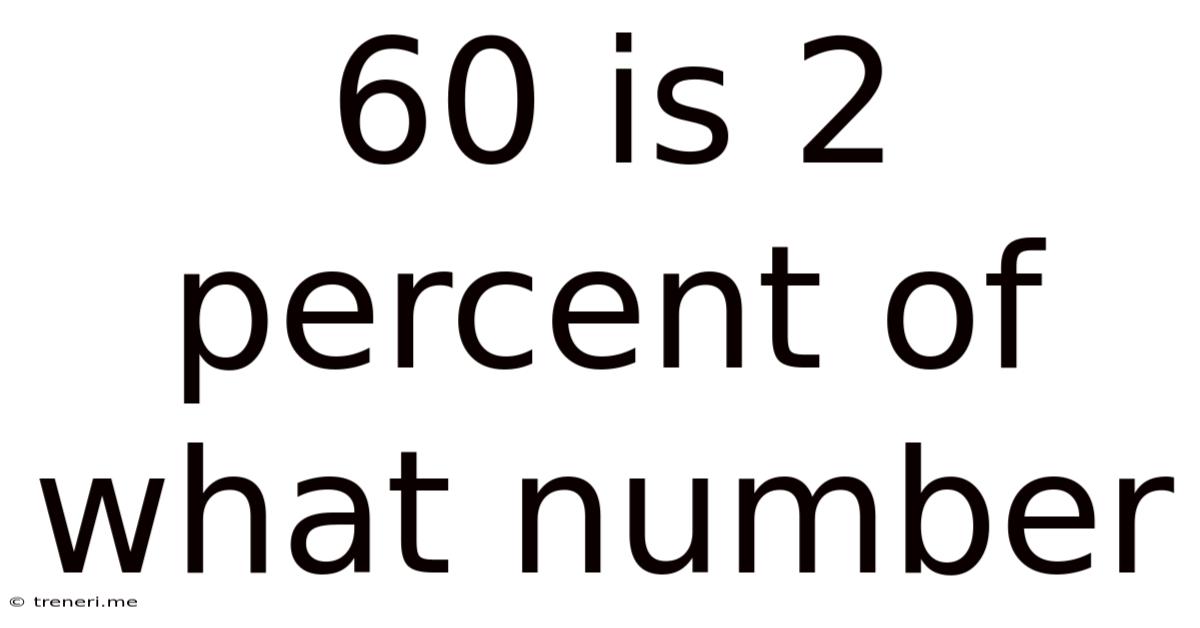
Table of Contents
60 is 2 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will delve into the specific problem of determining the base number when given a percentage and its corresponding value – in this case, finding the number of which 60 represents 2%. We'll explore multiple methods for solving this, clarifying the underlying concepts and providing practical examples to solidify your understanding.
Understanding the Fundamentals of Percentages
Before tackling the problem, let's establish a solid foundation in percentage calculations. A percentage is simply a fraction expressed as a part of 100. The percentage symbol (%) indicates this relationship. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key components in percentage calculations:
- The Percentage: This is the rate or proportion expressed as a percentage (e.g., 2%).
- The Part: This represents the value that corresponds to the given percentage (e.g., 60).
- The Whole (or Base): This is the total value of which the part is a percentage (This is what we need to find in our problem).
The standard formula relating these components is:
(Percentage/100) * Whole = Part
We can rearrange this formula to solve for any of the three components. In our case, we need to solve for the "Whole," which represents the number of which 60 is 2%.
Method 1: Solving the Equation Algebraically
Let's represent the unknown number (the whole) as 'x'. We can express the problem as an algebraic equation:
(2/100) * x = 60
To solve for x, we follow these steps:
- Multiply both sides by 100: This eliminates the fraction on the left side. The equation becomes:
2 * x = 6000
- Divide both sides by 2: This isolates 'x' and gives us the solution:
x = 3000
Therefore, 60 is 2% of 3000.
Method 2: Using Proportions
Another effective approach is to utilize proportions. We can set up a proportion to express the relationship between the percentage, the part, and the whole:
2/100 = 60/x
To solve this proportion, we cross-multiply:
2 * x = 60 * 100
2x = 6000
x = 3000
Again, we find that 60 is 2% of 3000. This method provides an alternative perspective and reinforces the solution.
Method 3: Utilizing the Percentage Formula Directly
We can directly manipulate the percentage formula:
(Percentage/100) * Whole = Part
We know:
- Part = 60
- Percentage = 2
Substituting these values into the formula:
(2/100) * x = 60
Solving for x:
x = (60 * 100) / 2 x = 6000 / 2 x = 3000
Once again, we arrive at the answer: 60 is 2% of 3000. This approach demonstrates the direct application of the fundamental percentage formula.
Practical Applications and Real-World Scenarios
Understanding percentage calculations, particularly finding the whole from a given part and percentage, is invaluable in many situations. Here are some real-world examples:
-
Finance: Calculating the principal amount of a loan based on the interest earned. For instance, if you earned $60 in interest at a 2% interest rate, you can use this method to find the principal amount.
-
Sales and Discounts: Determining the original price of an item after a discount. If an item is discounted by 2% and the discount amount is $60, you can use this calculation to find the original price.
-
Statistics and Data Analysis: Calculating the total population based on a sample percentage. For example, if a survey shows 2% of respondents (60 people) chose a specific option, this calculation will help to determine the total number of respondents.
-
Scientific Research: Determining total quantities based on percentages in experiments. For example, if 2% of a sample of cells (60 cells) exhibit a specific characteristic, this method can be used to estimate the total cell population.
-
Everyday Budgeting: Calculating your total income based on savings. Suppose 2% of your total income is $60 in savings. This calculation helps find your total income.
Common Mistakes to Avoid
While the process seems straightforward, several common mistakes can lead to incorrect results:
-
Incorrect Formula Manipulation: Ensure you correctly manipulate the percentage formula when solving for an unknown variable. A simple error in rearranging the equation will yield a wrong answer.
-
Calculation Errors: Double-check your arithmetic. Simple mistakes in multiplication and division can lead to significant errors in the final result.
-
Misunderstanding the Problem: Carefully read the problem statement to identify the known variables and the unknown quantity you need to find. Misinterpreting the question will result in an incorrect approach.
-
Ignoring Units: While not directly relevant in this particular problem, always pay attention to the units involved in more complex percentage problems. Incorrect unit handling can invalidate the result.
Expanding Your Understanding: Working with Different Percentages and Values
The method demonstrated here is adaptable to problems involving different percentages and values. For example, to find what number 15 is 5% of, you would simply substitute these values into the formula:
(5/100) * x = 15
Solving for x, you’d find x = 300. This highlights the versatility of the approach.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is crucial for various aspects of life. This article provided a detailed explanation of how to determine the base number when given a percentage and its value, using multiple methods to solidify understanding. By understanding the underlying concepts and practicing with different examples, you can confidently tackle percentage problems and apply them to real-world situations. Remember to always double-check your work and avoid common calculation errors to ensure accuracy. With consistent practice, you'll become proficient in solving percentage-related challenges and use this knowledge to make informed decisions in your personal and professional life.
Latest Posts
Latest Posts
-
How Long Is 77 Days In Months
May 12, 2025
-
Greatest Common Factor Of 26 And 34
May 12, 2025
-
104 Km Is Equal To How Many M
May 12, 2025
-
Cuanto Es 400 Libras En Kilos
May 12, 2025
-
Cuantos Dias Pasaron Desde El 19 De Julio Hasta Hoy
May 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 2 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.