60 Is 40 Percent Of What Number
Treneri
May 13, 2025 · 5 min read
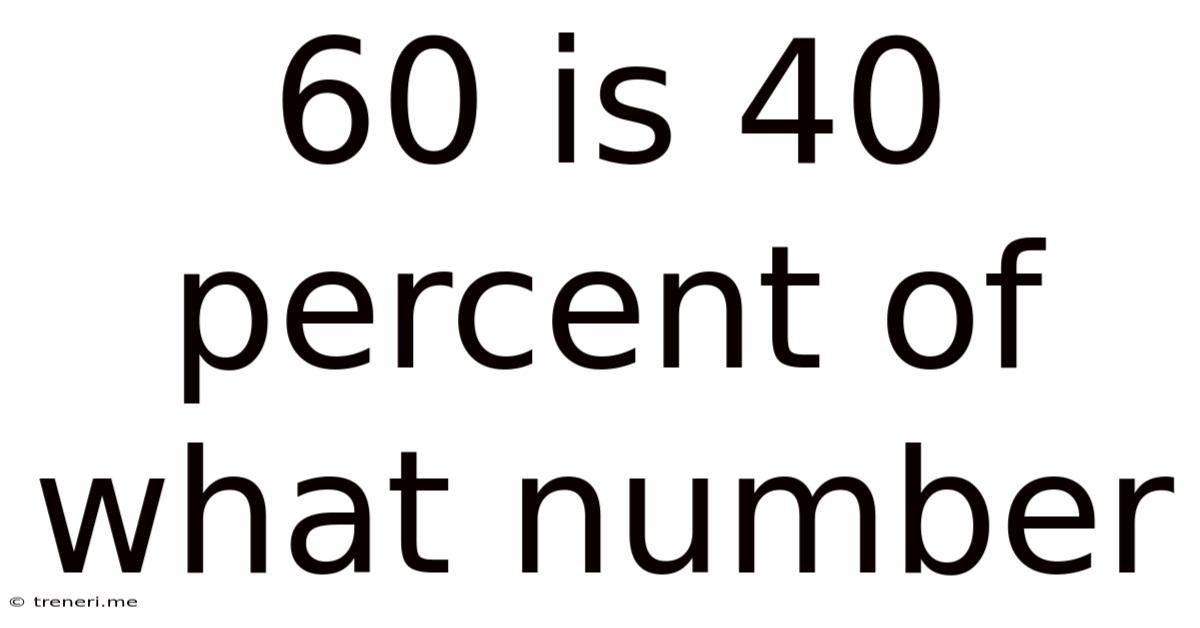
Table of Contents
60 is 40 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting and shopping to complex scientific calculations and financial analysis. Understanding how to find the whole when given a percentage and its corresponding part is crucial. This article comprehensively explores how to solve the problem "60 is 40 percent of what number," detailing multiple approaches and providing valuable insights into percentage calculations. We'll cover the fundamental concepts, delve into different solution methods, and explore real-world applications.
Understanding Percentages: The Basics
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 40% means 40 out of 100, or 40/100, which simplifies to 2/5.
This understanding is crucial because percentage problems essentially involve relationships between three quantities:
- The Part: This is the portion of the whole that's given (in our case, 60).
- The Percentage: This is the rate, often expressed as a percentage (in our case, 40%).
- The Whole: This is the total amount we're trying to find.
The fundamental relationship is expressed as:
(Part / Whole) * 100% = Percentage
Method 1: Using the Formula
The most straightforward method to solve "60 is 40 percent of what number" is by using the basic percentage formula and rearranging it to solve for the unknown (the whole).
Let's represent:
- Part = 60
- Percentage = 40% = 0.40 (Remember to convert percentages to decimals by dividing by 100)
- Whole = x (This is what we need to find)
Our formula becomes:
60 / x = 0.40
To solve for x, we can follow these steps:
- Multiply both sides by x: 60 = 0.40x
- Divide both sides by 0.40: x = 60 / 0.40
- Calculate: x = 150
Therefore, 60 is 40 percent of 150.
Method 2: Using Proportions
Another effective way to solve percentage problems is by setting up a proportion. A proportion expresses the equality of two ratios. We can express the given information as two equivalent ratios:
60/x = 40/100
This proportion states that the ratio of the part (60) to the whole (x) is equal to the ratio of the percentage (40) to 100.
To solve this proportion, we can use cross-multiplication:
60 * 100 = 40 * x
6000 = 40x
x = 6000 / 40
x = 150
This method confirms that 60 is 40 percent of 150.
Method 3: The Unitary Method
The unitary method focuses on finding the value of one unit (in this case, 1%) before scaling up to find the whole.
- Find 1%: If 40% is equal to 60, then 1% would be 60 / 40 = 1.5
- Find 100%: To find the whole (100%), we multiply the value of 1% by 100: 1.5 * 100 = 150
This method again shows that 60 is 40 percent of 150.
Real-World Applications
Understanding percentage calculations is essential in numerous real-world scenarios:
- Finance: Calculating interest, discounts, taxes, profit margins, and investment returns all involve percentage calculations. For example, understanding how much of a total investment represents a specific percentage return is key to evaluating investment performance.
- Shopping: Determining the final price after a discount, comparing prices, and understanding sales tax all rely on percentage calculations. Being able to quickly calculate discounts helps make informed purchasing decisions.
- Science: Many scientific calculations and data analysis involve percentages. For example, expressing experimental results as percentages or calculating statistical significance relies on this mathematical skill.
- Data Analysis: Percentages are used extensively in representing data in charts, graphs, and tables. For instance, expressing survey results or market share data often involves percentages.
- Everyday Life: Calculating tips, splitting bills, and understanding increases or decreases in quantities (like population growth or price changes) all involve percentage concepts.
Tips for Solving Percentage Problems
- Convert Percentages to Decimals: Always convert percentages to decimals (divide by 100) before performing calculations. This simplifies the process and minimizes errors.
- Identify the Unknown: Clearly identify what quantity you need to find (the part, the percentage, or the whole).
- Choose the Right Method: Select the method that you find most comfortable and efficient. All the methods discussed above will produce the same accurate results.
- Check Your Work: After calculating the answer, check if it logically makes sense in the context of the problem. Does the answer seem reasonable given the values provided?
- Practice Regularly: The more you practice solving percentage problems, the more confident and efficient you'll become.
Beyond the Basics: More Complex Percentage Problems
The example "60 is 40 percent of what number" is a relatively simple percentage problem. However, the core concepts can be extended to solve more complex scenarios, involving multiple percentages, consecutive increases or decreases, and compound interest calculations. Mastering the fundamental principles of percentage calculations provides a solid foundation for tackling these more advanced problems.
Conclusion
Understanding how to solve "60 is 40 percent of what number" and similar percentage problems is a critical skill with wide-ranging applications. By understanding the fundamental concepts, mastering the different solution methods (using formulas, proportions, or the unitary method), and practicing regularly, you can confidently tackle percentage calculations in various aspects of your life, both personal and professional. The ability to perform these calculations efficiently improves decision-making, promotes accuracy, and enhances your overall numerical literacy. Remember, consistent practice is key to mastering this essential skill.
Latest Posts
Latest Posts
-
Water Density At 23 Degrees Celsius
May 13, 2025
-
Dilution Ratios For 16 Oz Bottle
May 13, 2025
-
2143 57 Rounded To The Nearest Hundredth
May 13, 2025
-
How Many Pints To A Gallon Us
May 13, 2025
-
4 To The Power Of 15
May 13, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 40 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.