62 Divided By What Equals 31
Treneri
Apr 26, 2025 · 5 min read
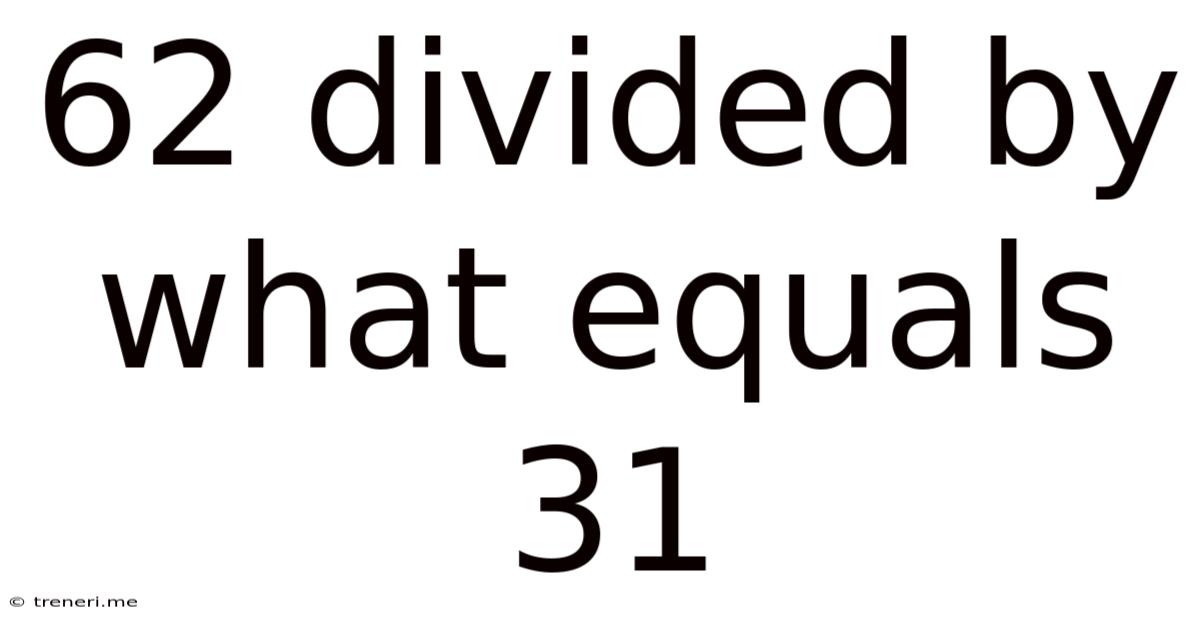
Table of Contents
Unraveling the Mystery: 62 Divided by What Equals 31? A Deep Dive into Division
The simple question, "62 divided by what equals 31?" might seem trivial at first glance. However, exploring this seemingly basic arithmetic problem opens doors to a deeper understanding of division, its applications, and its connection to broader mathematical concepts. This article will not only answer the initial question but also delve into the underlying principles, explore related problems, and even touch upon the practical applications of division in everyday life and advanced fields.
Finding the Answer: A Straightforward Approach
The most direct way to solve "62 divided by what equals 31" is to use the fundamental concept of division: division is the inverse operation of multiplication. If we represent the unknown number as 'x', the problem can be written as an equation:
62 / x = 31
To solve for 'x', we can use algebraic manipulation. Multiply both sides of the equation by 'x':
62 = 31x
Now, divide both sides by 31:
x = 62 / 31
Therefore, x = 2.
62 divided by 2 equals 31. This is the straightforward answer to our initial question.
Understanding Division: More Than Just Sharing
While finding the answer is simple, understanding why this works is crucial. Division, at its core, represents the process of splitting a quantity into equal parts. In this case, we're splitting 62 into equal parts, resulting in 31 in each part. This concept has numerous real-world applications:
-
Sharing Equally: Imagine 62 candies to be shared equally among a group of children. If each child receives 31 candies, there must be 2 children in the group.
-
Rate and Ratio: If a car travels 62 miles in a certain time, and its average speed is 31 miles per hour, then the journey took 2 hours.
-
Scaling and Proportion: In recipes, if a recipe calls for 62 grams of flour and you want to halve the recipe, you would use 31 grams, implying a scaling factor of 1/2.
Exploring Related Problems and Variations
The original problem can be extended and modified to explore related mathematical concepts:
1. Changing the Dividend: What if we changed the number 62? For example:
-
124 divided by what equals 31? Following the same approach, we get: 124 / x = 31, which leads to x = 4.
-
31 divided by what equals 31? This results in x = 1.
These examples highlight the relationship between the dividend (the number being divided) and the result. As the dividend increases (while the quotient remains constant), the divisor decreases.
2. Changing the Quotient: What if we changed the result (31)? For instance:
-
62 divided by what equals 62? This gives x = 1.
-
62 divided by what equals 1? This results in x = 62.
These variations demonstrate the inverse relationship between the quotient and the divisor. As the desired quotient increases, the divisor decreases, and vice-versa.
3. Introducing Fractions: The problem can also be expressed using fractions:
- What fraction of 62 is 31? This is equivalent to 31/62 which simplifies to 1/2. This shows the connection between division and fractions.
4. Applying Algebra: We can generalize the problem using variables. If 'a' divided by 'b' equals 'c', then the equation is a/b = c. This can be rearranged to solve for any of the variables. This is a fundamental concept in algebra.
Advanced Applications and Extensions
The seemingly simple division problem can be extended into more complex mathematical concepts:
-
Modular Arithmetic: Division plays a crucial role in modular arithmetic (clock arithmetic), where the remainder after division is the focus.
-
Calculus: Division is fundamental to various calculus operations, including differentiation and integration.
-
Linear Algebra: Division is used extensively in solving systems of linear equations and performing matrix operations.
-
Computer Science: Division is a core operation in computer programming, used for various tasks such as data manipulation, array indexing, and algorithm design.
Real-World Applications: Beyond the Classroom
Division is far from a purely academic exercise; it is integrated into various aspects of daily life:
-
Finance: Calculating interest rates, splitting bills, budgeting, and determining unit prices all involve division.
-
Cooking and Baking: Scaling recipes, converting units, and calculating ingredient ratios require proficiency in division.
-
Construction and Engineering: Dividing lengths, areas, and volumes are crucial aspects of construction and engineering projects.
-
Data Analysis: Calculating averages, percentages, and ratios in data analysis relies heavily on division.
-
Science: Numerous scientific calculations, including determining speeds, concentrations, and densities, require division.
Mastering Division: Tips and Tricks
While the basic concept is relatively straightforward, mastering division requires practice and understanding the underlying principles. Here are a few helpful tips:
-
Practice Regularly: The more you practice, the faster and more accurate you will become.
-
Understand the Relationship Between Division and Multiplication: The inverse relationship between these two operations is key to solving division problems.
-
Learn Different Division Methods: Explore various methods, such as long division, short division, and mental math techniques.
-
Use Calculators Strategically: Calculators can be useful for complex calculations, but understanding the underlying principles remains crucial.
-
Break Down Complex Problems: Divide larger problems into smaller, manageable steps.
Conclusion: The Power of Division
The seemingly simple question, "62 divided by what equals 31?" provides a gateway to a vast world of mathematical concepts and practical applications. Understanding division is not merely about performing a calculation; it's about grasping a fundamental principle that underpins countless aspects of our lives, from everyday tasks to complex scientific and engineering endeavors. By exploring this seemingly simple question, we've uncovered the richness and versatility of division, its role in different mathematical fields, and its widespread relevance in the real world. Mastering division is a valuable skill that empowers you to tackle a wide range of challenges and problems with confidence.
Latest Posts
Latest Posts
-
180 Days From January 26 2024
May 09, 2025
-
Que Es El Apy En Banco
May 09, 2025
-
Cuantos Pies Son En 20 Metros
May 09, 2025
-
How Many Shingle Bundles On A Pallet
May 09, 2025
-
6 To 8 Oz Of Water
May 09, 2025
Related Post
Thank you for visiting our website which covers about 62 Divided By What Equals 31 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.