66 Out Of 80 As A Percentage
Treneri
May 10, 2025 · 5 min read
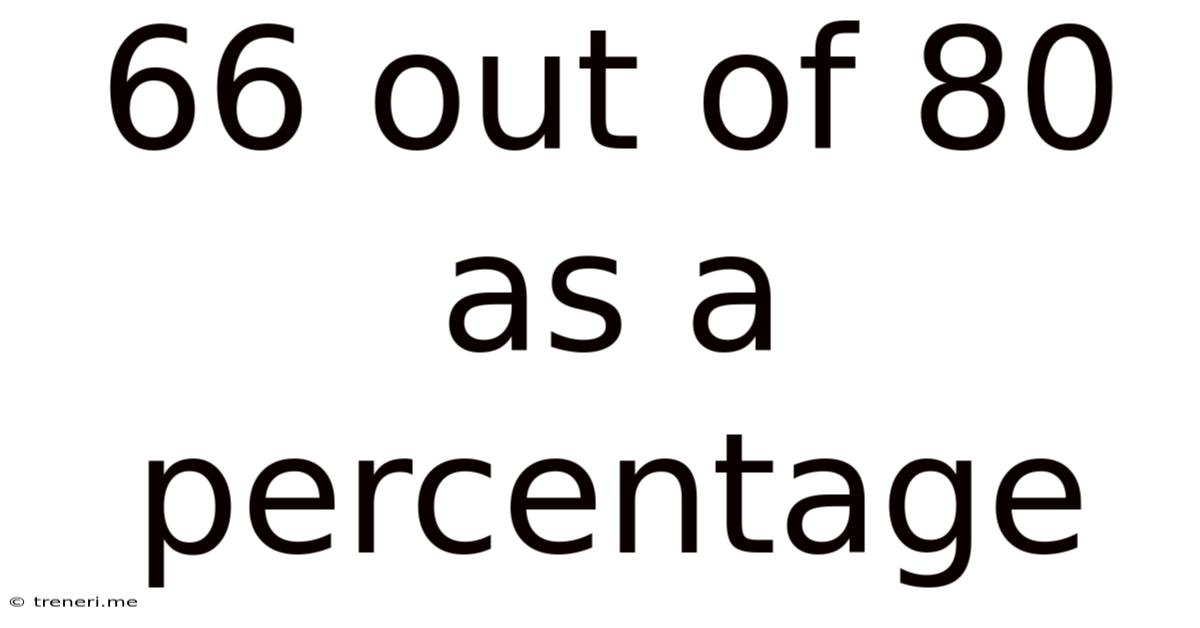
Table of Contents
66 out of 80 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with wide-ranging applications, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions into percentages is crucial for various fields, including academics, finance, and business. This article dives deep into calculating "66 out of 80 as a percentage," explaining the process step-by-step, exploring different calculation methods, and providing practical examples to solidify your understanding. We'll also touch upon the broader applications of percentage calculations and how they relate to other mathematical concepts.
Understanding Percentages
Before tackling the specific calculation, let's clarify the concept of percentages. A percentage represents a fraction of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Calculating 66 out of 80 as a Percentage: The Step-by-Step Method
The most straightforward way to calculate 66 out of 80 as a percentage involves these three simple steps:
Step 1: Set up the Fraction
First, express the given numbers as a fraction. In this case, 66 is the part, and 80 is the whole. Therefore, the fraction is 66/80.
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (66) by the denominator (80):
66 ÷ 80 = 0.825
Step 3: Convert the Decimal to a Percentage
Multiply the decimal by 100 to express it as a percentage:
0.825 × 100 = 82.5%
Therefore, 66 out of 80 is 82.5%.
Alternative Calculation Methods
While the above method is the most common, other approaches can achieve the same result. Let's explore a couple of alternatives:
Method 1: Using Proportions
Proportions provide an alternative method to solve this problem. We can set up a proportion where x represents the percentage:
x/100 = 66/80
Cross-multiplying gives:
80x = 6600
Dividing both sides by 80 gives:
x = 82.5
Therefore, 66 out of 80 is 82.5%.
Method 2: Simplifying the Fraction First
Before converting to a decimal, simplifying the fraction can sometimes make the calculation easier. Both 66 and 80 are divisible by 2:
66/80 = 33/40
Now, divide 33 by 40:
33 ÷ 40 = 0.825
Multiply by 100 to obtain the percentage:
0.825 × 100 = 82.5%
This method demonstrates that simplifying the fraction before the decimal conversion can sometimes simplify the arithmetic.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios. Here are a few examples:
-
Academic Performance: Calculating grades, often expressed as percentages, is a common application. If a student scores 66 out of 80 on a test, their percentage score is 82.5%, providing a clear understanding of their performance relative to the total possible marks.
-
Financial Calculations: Percentages are fundamental in finance. Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating discounts, tax rates, and profit margins also heavily relies on percentage calculations. For example, a 10% discount on an item priced at $100 results in a $10 discount, bringing the final price down to $90.
-
Data Analysis and Statistics: In statistical analysis, percentages are used to represent proportions and probabilities. For example, a survey might reveal that 82.5% of respondents prefer a particular product, providing valuable insights for market research and business decisions.
-
Business and Economics: Percentages are used extensively in business to track growth rates, market share, and various key performance indicators (KPIs). For example, a company's year-over-year revenue growth can be expressed as a percentage, allowing for easy comparison and trend analysis.
-
Everyday Life: We encounter percentages daily, from sales discounts at stores to tips in restaurants and nutritional information on food labels. Understanding percentages allows us to make informed decisions and manage our finances effectively.
Beyond the Basics: Advanced Percentage Concepts
While calculating 66 out of 80 as a percentage is a relatively straightforward task, delving deeper into percentage-related concepts can broaden your mathematical understanding and problem-solving abilities. Here are a few areas to explore further:
-
Percentage Increase and Decrease: Calculating the percentage increase or decrease between two values is a common task in many fields. For instance, if a product's price increases from $100 to $120, the percentage increase is 20%. Conversely, if it decreases from $120 to $100, the percentage decrease is also 20%.
-
Percentage Points: It's crucial to differentiate between percentages and percentage points. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself. This distinction is vital for clear communication and accurate analysis.
-
Compound Interest: Compound interest involves earning interest not only on the principal amount but also on accumulated interest. Understanding compound interest is crucial for long-term investment planning and understanding the growth potential of savings accounts and investments.
-
Percentage Change and Rate of Change: This expands on percentage increase and decrease, focusing on analyzing trends and patterns over time. Understanding rate of change is critical in various fields including economics, finance, and environmental science.
-
Applying percentages to complex equations and formulas: Percentages often form part of more complex mathematical models in fields such as actuarial science, engineering, and statistics.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages accurately and efficiently is a valuable skill applicable across numerous contexts. While the process of calculating 66 out of 80 as a percentage might seem simple, understanding the underlying principles and various calculation methods empowers you to tackle more complex percentage-related problems. By mastering these fundamental concepts and exploring related advanced topics, you significantly enhance your mathematical proficiency and practical problem-solving skills. Remember to practice regularly to reinforce your understanding and build confidence in your abilities. The more you practice, the more intuitive these calculations will become, enabling you to confidently navigate percentage-related challenges in your academic, professional, and personal life.
Latest Posts
Latest Posts
-
Find An Expression For The Perimeter Of The Figure
May 10, 2025
-
1 Barra De Mantequilla Cuantos Gramos Son
May 10, 2025
-
Cuanto Es 40 Pulgadas En Pies
May 10, 2025
-
64 Months Is How Many Years
May 10, 2025
-
How To Convert Joules To Nanometers
May 10, 2025
Related Post
Thank you for visiting our website which covers about 66 Out Of 80 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.