7 1 2 In Radical Form
Treneri
May 11, 2025 · 4 min read
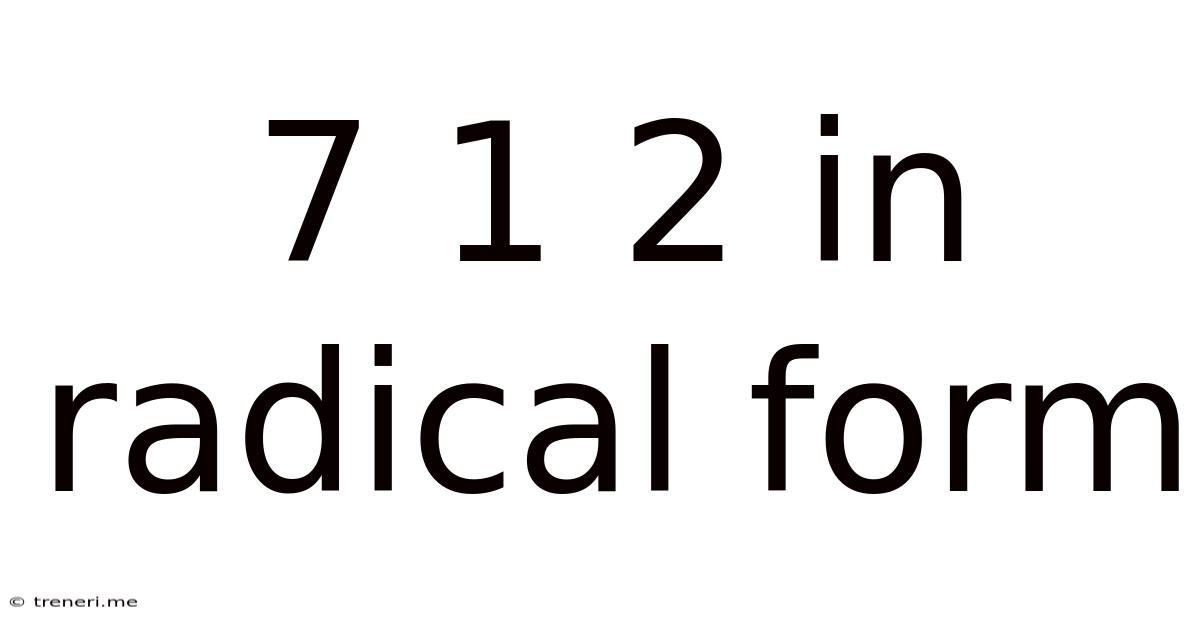
Table of Contents
7 1 2 in Radical Form: A Comprehensive Exploration
The expression "7 1 2 in radical form" is not mathematically precise. It's likely referring to the conversion of the mixed number 7 1/2 into a radical expression. However, there's no single "radical form" for 7 1/2, as the process depends on how we choose to manipulate the number. This article will explore various approaches, delve into the underlying mathematical principles, and offer a comprehensive understanding of how to represent 7 1/2 using radicals, including potential interpretations and relevant mathematical concepts.
Understanding Mixed Numbers and Radicals
Before we begin, let's clarify the terminology:
-
Mixed Number: A mixed number combines a whole number and a fraction, like 7 1/2.
-
Radical (or Root): A radical expresses a number's root, indicated by the radical symbol (√). The number inside the radical is called the radicand. For example, √9 represents the square root of 9, which is 3. The small number in the "v" shape (called the index) indicates the root being taken (square root, cube root, etc). If no index is written, it's implicitly a square root (index of 2).
Converting 7 1/2 to an Improper Fraction
The first step in expressing 7 1/2 in any radical form is to convert it into an improper fraction. This simplifies subsequent manipulations:
7 1/2 = (7 × 2 + 1) / 2 = 15/2
This means 7 1/2 is equivalent to 15 halves. This improper fraction form is crucial for various radical manipulations.
Method 1: Expressing as a Square Root
We can't directly express 15/2 as a simple square root. The square root of a fraction is the square root of the numerator divided by the square root of the denominator:
√(15/2) = √15 / √2
This is a perfectly valid radical representation of 7 1/2, but it's not fully simplified. To simplify further, we need to rationalize the denominator.
Rationalizing the Denominator:
Rationalizing involves eliminating the radical from the denominator. We do this by multiplying both the numerator and the denominator by √2:
(√15 / √2) × (√2 / √2) = √30 / 2
Therefore, one radical representation of 7 1/2 is √30 / 2.
Method 2: Exploring Higher Roots
While square roots are the most common radicals, we can explore higher-order roots as well. For example, we can express 7 1/2 as a cube root, fourth root, and so on. However, these representations won't necessarily be simpler or more intuitive than the square root form.
Let's consider the cube root:
We need to find a number 'x' such that x³ = 15/2. This doesn't yield a neat integer or simple radical expression. Similar situations arise with higher roots.
Method 3: Using Fractional Exponents
Another approach involves using fractional exponents, which are closely related to radicals:
15/2 can be written as (15/2)^1. This can be expressed with any exponent as long as it's equivalent to 1.
We can use fractional exponents to represent radicals. For example:
√x = x^(1/2) (square root) ∛x = x^(1/3) (cube root) ⁴√x = x^(1/4) (fourth root)
Applying this to 15/2:
(15/2)^(1/2) = √(15/2) = √30/2
This reinforces the result we obtained using the square root method and rationalization.
Advanced Considerations and Extensions
Approximations:
While we've explored exact radical forms, it's important to remember that irrational numbers like √30 don't have a finite decimal representation. Calculators can provide approximations:
√30 ≈ 5.477
Therefore, √30/2 ≈ 2.7385
This approximation is useful for practical calculations.
Context Matters:
The "best" radical representation of 7 1/2 depends on the context. In certain algebraic manipulations, √30/2 might be preferable. In others, the approximation 2.7385 could be more convenient.
Exploring Different Bases:
While we focused on base 10, the concepts apply to other number bases. Converting 7 1/2 to a different base and then expressing it in radical form within that base would yield a different result, though mathematically equivalent.
Application in Geometry and Other Fields:
Radical expressions frequently appear in geometric calculations, such as finding the lengths of diagonals in squares or calculating areas of triangles. Understanding how to manipulate radicals is crucial in such scenarios. Similarly, the conversion of mixed numbers to radical forms can be useful in calculus and physics, particularly where irrational numbers frequently arise.
Conclusion
While the initial prompt "7 1/2 in radical form" may seem straightforward, it reveals the richness of mathematical representation. There's no single "correct" answer; the optimal radical form depends on the context and desired level of simplification. This exploration has demonstrated how to convert 7 1/2 into various radical expressions using different methods, including simplifying radicals, rationalizing denominators, and utilizing fractional exponents. Mastering these techniques is crucial for success in various mathematical and scientific disciplines. Remember that understanding the underlying mathematical principles, such as rationalization and the relationship between radicals and fractional exponents, provides a solid foundation for tackling more complex problems involving radicals in the future. The ability to choose the most appropriate representation based on the context is a hallmark of advanced mathematical thinking.
Latest Posts
Latest Posts
-
Cuantos Dias Faltan Para El 21 De Diciembre
May 12, 2025
-
Can You Tan In A Uv Of 3
May 12, 2025
-
Convertir 100 Grados Fahrenheit A Celsius
May 12, 2025
-
855 Divided By 45 With Remainder
May 12, 2025
-
How To Calculate Income Tax Return In Philippines
May 12, 2025
Related Post
Thank you for visiting our website which covers about 7 1 2 In Radical Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.