7/9 Is Equivalent To What Fraction
Treneri
May 15, 2025 · 5 min read
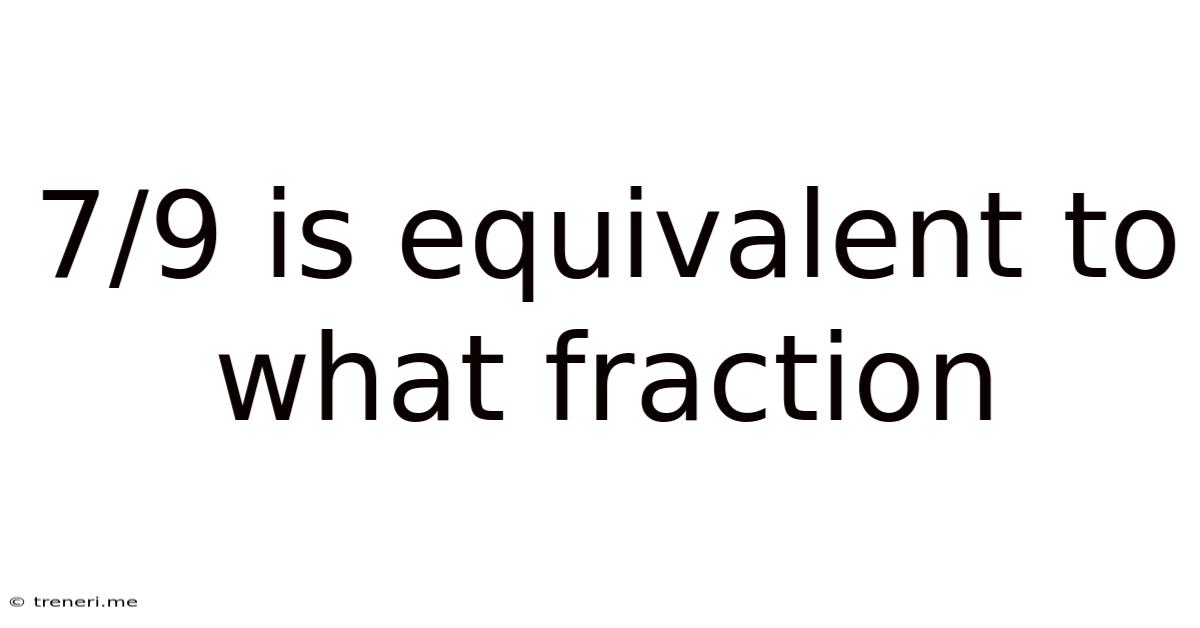
Table of Contents
7/9 is Equivalent to What Fraction? Exploring Equivalent Fractions and Their Applications
The question, "7/9 is equivalent to what fraction?" might seem deceptively simple. However, understanding equivalent fractions is fundamental to mastering arithmetic, algebra, and even more advanced mathematical concepts. This comprehensive guide will not only answer this specific question but also delve into the broader world of equivalent fractions, exploring their properties, how to find them, and their practical applications.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. Imagine cutting a pizza into 9 slices and taking 7. That's 7/9 of the pizza. Now imagine cutting the same pizza into 18 slices; you'd need to take 14 slices to have the same amount of pizza (7/9 = 14/18). Both fractions represent the same portion of the whole.
Key Principle: Equivalent fractions are created by multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number.
This principle is crucial. Multiplying or dividing by 1 (in the form of, say, 2/2 or 3/3) doesn't change the value of the fraction because it's essentially multiplying by one. This is why we can find countless equivalent fractions for any given fraction.
Finding Equivalent Fractions for 7/9
To find equivalent fractions for 7/9, we simply multiply both the numerator and denominator by the same number. Let's explore some examples:
- Multiplying by 2: (7 x 2) / (9 x 2) = 14/18
- Multiplying by 3: (7 x 3) / (9 x 3) = 21/27
- Multiplying by 4: (7 x 4) / (9 x 4) = 28/36
- Multiplying by 5: (7 x 5) / (9 x 5) = 35/45
- Multiplying by 10: (7 x 10) / (9 x 10) = 70/90
And so on. You can continue this process indefinitely, generating an infinite number of equivalent fractions for 7/9. Each fraction represents the same proportion—7 out of 9 parts.
Simplifying Fractions: Finding the Simplest Form
While we can create infinitely many equivalent fractions, often we want the simplest form. The simplest form of a fraction is when the numerator and denominator have no common factors other than 1. This is also known as reducing the fraction to its lowest terms.
To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both numbers without leaving a remainder. Then, we divide both the numerator and denominator by the GCD.
Let's consider the fraction 14/18. The factors of 14 are 1, 2, 7, and 14. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest common divisor of 14 and 18 is 2.
Therefore, to simplify 14/18, we divide both the numerator and denominator by 2:
14/2 = 7 and 18/2 = 9
This simplifies 14/18 to 7/9, which is the simplest form. Notice that 7/9 has already been reduced to its simplest form.
Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in numerous mathematical applications and real-world scenarios:
-
Adding and Subtracting Fractions: Before adding or subtracting fractions, you often need to find equivalent fractions with a common denominator. For example, adding 1/2 and 1/3 requires finding equivalent fractions with a denominator of 6: 1/2 = 3/6 and 1/3 = 2/6.
-
Comparing Fractions: Determining which fraction is larger requires finding equivalent fractions with a common denominator.
-
Ratios and Proportions: Equivalent fractions are fundamental to understanding ratios and proportions, which are essential in various fields like cooking, scaling drawings, and solving problems involving percentages.
-
Decimals and Percentages: Fractions can be easily converted to decimals and percentages. For example, 7/9 is approximately 0.777... (a recurring decimal) and 77.77% (rounded).
-
Algebra: Equivalent fractions play a crucial role in solving algebraic equations involving fractions.
-
Geometry and Measurement: Fractions are essential for calculations related to areas, volumes, and other geometric properties.
Beyond 7/9: Mastering Equivalent Fractions
The process of finding equivalent fractions and simplifying them applies to any fraction. The key principle always remains the same: multiply or divide both the numerator and the denominator by the same non-zero number.
Let's take another example: the fraction 4/6.
-
Simplifying: The GCD of 4 and 6 is 2. Dividing both by 2 gives 2/3. This is the simplest form.
-
Finding equivalents: Multiplying both the numerator and denominator by 3 gives 12/18. Multiplying by 5 gives 20/30. And so on.
The ability to effortlessly work with equivalent fractions is a cornerstone of mathematical proficiency. It empowers you to simplify expressions, solve equations, and tackle a wide range of problems with confidence.
Practical Exercises:
To solidify your understanding, try these exercises:
- Find three equivalent fractions for 5/8.
- Simplify the fraction 15/25 to its simplest form.
- Find a common denominator for the fractions 2/3 and 3/4, and then add them.
- Convert the fraction 3/5 into a decimal and a percentage.
- Explain how understanding equivalent fractions helps in solving real-world problems.
By practicing these exercises and exploring various examples, you’ll significantly enhance your grasp of equivalent fractions and their widespread applications in mathematics and beyond. Remember the core principle: multiply or divide both the numerator and denominator by the same non-zero number to create an equivalent fraction. This simple yet powerful rule opens up a vast world of mathematical possibilities.
Latest Posts
Latest Posts
-
How Many Cups Are In A Lb Of Sugar
May 15, 2025
-
What Is The Gcf Of 90 And 36
May 15, 2025
-
Viscosity Of Water In Imperial Units
May 15, 2025
-
Greatest Common Factor Of 63 And 84
May 15, 2025
-
How To Find A Midpoint Of A Triangle
May 15, 2025
Related Post
Thank you for visiting our website which covers about 7/9 Is Equivalent To What Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.