7 Is What Percent Of 11
Treneri
May 10, 2025 · 5 min read
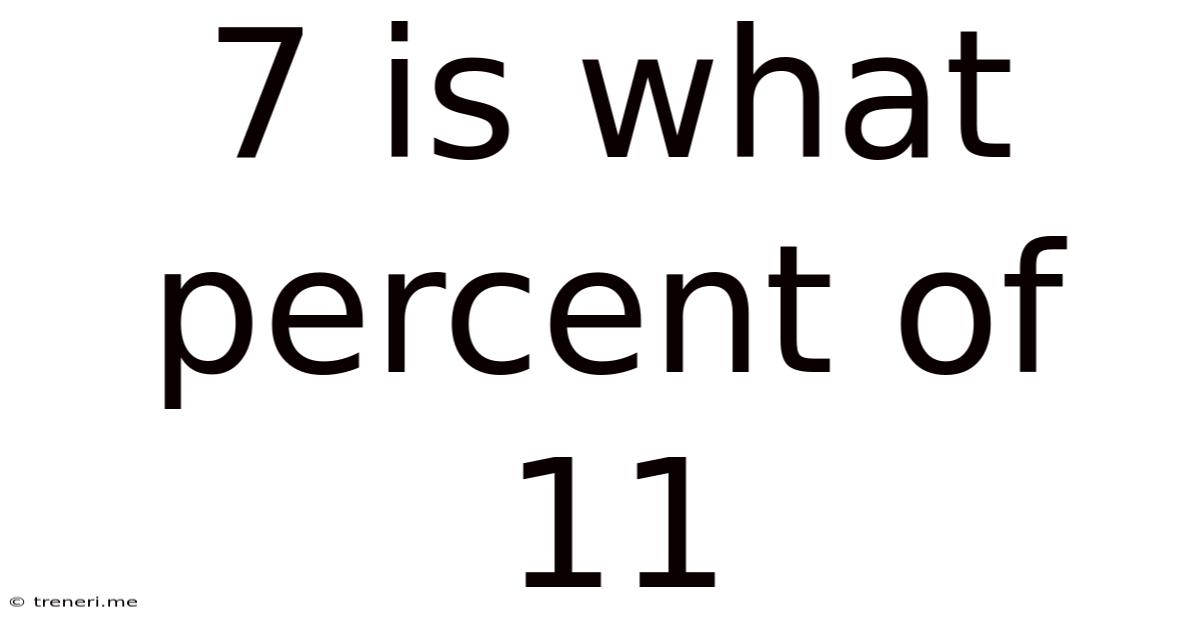
Table of Contents
7 is What Percent of 11? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only answer the question "7 is what percent of 11?" but also equip you with the knowledge and tools to tackle similar percentage problems with confidence. We'll explore the underlying concepts, delve into different calculation methods, and provide practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (per centum in Latin). For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used extensively because they provide a standardized way to compare proportions. Whether you're comparing sales figures, test scores, or the composition of a mixture, percentages offer a convenient and easily understood format.
Calculating Percentages: Three Key Methods
There are several ways to calculate percentages, each with its own advantages depending on the context and your familiarity with mathematical operations. Let's explore three common methods:
Method 1: Using the Percentage Formula
The most straightforward method involves using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In our specific problem, "7 is what percent of 11?", we identify:
- Part: 7
- Whole: 11
Substituting these values into the formula:
(7 / 11) x 100 = 63.6363...%
Therefore, 7 is approximately 63.64% of 11. We round to two decimal places for practicality.
Method 2: Using Proportions
This method involves setting up a proportion, which is an equation stating that two ratios are equal. We can express the problem as:
7/11 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
11x = 700
x = 700/11
x ≈ 63.64%
This method reinforces the underlying relationship between fractions and percentages.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation significantly. Simply enter 7 ÷ 11 x 100 and the calculator will directly provide the percentage. This is the most efficient method for quick calculations.
Applying Percentage Calculations: Real-World Examples
Understanding percentages extends far beyond simple mathematical problems. Let's explore how percentage calculations are relevant in various real-world scenarios:
1. Sales and Discounts:
Imagine a store offering a 20% discount on an item originally priced at $50. To calculate the discount amount:
(20/100) x $50 = $10
The discount is $10, and the final price is $50 - $10 = $40.
2. Tax Calculations:
Suppose a sales tax rate is 8%. To determine the tax on a $120 purchase:
(8/100) x $120 = $9.60
The sales tax is $9.60, and the total cost is $120 + $9.60 = $129.60.
3. Grade Calculations:
If a student scores 35 out of 50 on a test, their percentage score is:
(35/50) x 100 = 70%
4. Financial Analysis:
Percentages are crucial in analyzing financial statements. For instance, profit margins, return on investment (ROI), and debt-to-equity ratios are all expressed as percentages.
5. Data Analysis and Statistics:
In research and statistical analysis, percentages are used to represent proportions within datasets, making it easier to compare groups and identify trends. For example, expressing the percentage of respondents who favor a particular political candidate or the percentage change in a stock price over time.
Beyond the Basics: Advanced Percentage Concepts
While the core concept of percentages is relatively simple, there are several related concepts that build upon this foundation. Understanding these advanced concepts enhances your analytical capabilities and allows you to tackle more complex problems:
-
Percentage Increase/Decrease: Calculating the percentage change between two values, representing growth or decline. The formula is: [(New Value - Old Value) / Old Value] x 100.
-
Percentage Points: Represents the absolute difference between two percentages. For instance, if the unemployment rate increases from 5% to 8%, the increase is 3 percentage points, not 60%.
-
Compound Interest: Interest calculated on both the principal amount and accumulated interest from previous periods. This leads to exponential growth and is fundamental in understanding investments and loans.
-
Percentage of a Percentage: Calculating a percentage of a percentage involves multiplying the two percentages together and dividing by 100. For example, finding 10% of 20% is (10/100) * (20/100) *100 = 2%.
-
Reverse Percentage Calculations: Determining the original value when given the percentage and the final value. These often involve setting up equations and solving for the unknown variable.
Mastering Percentage Calculations: Tips and Practice
Consistent practice is key to mastering percentage calculations. Here are some tips to improve your skills:
-
Understand the Formula: Thoroughly grasp the fundamental percentage formula and how it applies to different situations.
-
Practice Regularly: Solve various percentage problems, starting with simple examples and gradually increasing the complexity.
-
Use Different Methods: Become comfortable using different calculation methods to solve problems, such as the formula, proportions, and calculators.
-
Visualize the Problem: Sometimes drawing a diagram or using visual aids can help you understand the relationships between the parts and the whole.
-
Check Your Answers: Always double-check your calculations to ensure accuracy.
Conclusion: The Power of Percentages
The ability to calculate and interpret percentages is a highly valuable skill applicable to numerous fields. From everyday financial transactions to advanced statistical analysis, a firm grasp of percentages enables confident decision-making and a deeper understanding of the world around us. By mastering the concepts and techniques outlined in this guide, you'll be well-equipped to tackle any percentage-related challenge with ease and precision. Remember that consistent practice and application are key to building proficiency in this essential mathematical skill. The seemingly simple question, "7 is what percent of 11?" opens the door to a world of quantitative understanding and problem-solving.
Latest Posts
Latest Posts
-
Time In A Half For 18
May 10, 2025
-
98 Rounded To The Nearest Ten
May 10, 2025
-
How Many Minutes Are In 2 Years
May 10, 2025
-
Greatest Common Factor Of 32 And 45
May 10, 2025
-
How Old Is 1981 In 2024
May 10, 2025
Related Post
Thank you for visiting our website which covers about 7 Is What Percent Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.