7 Is What Percent Of 24
Treneri
May 11, 2025 · 4 min read
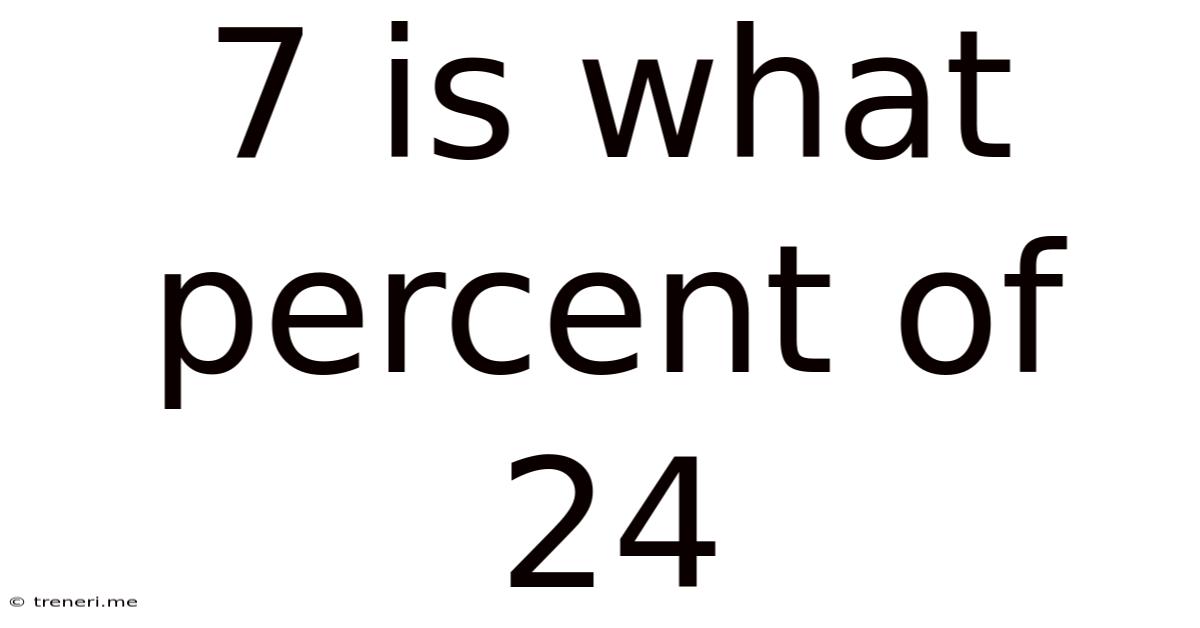
Table of Contents
7 is What Percent of 24? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will delve into the question, "7 is what percent of 24?", providing not just the answer but a deep dive into the methodology, practical applications, and related concepts. We'll explore different calculation methods, address common misconceptions, and equip you with the knowledge to tackle similar percentage problems with confidence.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's establish a solid foundation in percentage calculations. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" represents "per hundred." For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5 as a decimal.
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
Where:
- Part: Represents the specific value you're interested in expressing as a percentage.
- Whole: Represents the total value.
Calculating "7 is What Percent of 24?"
Now, let's apply this formula to our specific question: "7 is what percent of 24?"
In this scenario:
- Part = 7
- Whole = 24
Using the formula:
(7 / 24) * 100 = Percentage
Performing the calculation:
0.291666... * 100 ≈ 29.17%
Therefore, 7 is approximately 29.17% of 24.
Alternative Calculation Methods
While the above method is straightforward, there are alternative approaches to calculating percentages. Understanding these alternative methods can enhance your problem-solving skills and provide flexibility depending on the context.
Method 2: Using Proportions
Proportions offer a visually intuitive way to solve percentage problems. We can set up a proportion as follows:
7/24 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
7 * 100 = 24 * x
700 = 24x
x = 700 / 24
x ≈ 29.17%
This method reinforces the underlying relationship between fractions and percentages.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal first and then multiplying by 100.
7/24 ≈ 0.2917
0.2917 * 100 ≈ 29.17%
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
- Retail Discounts: Calculating the price reduction during sales events. For example, a 20% discount on a $50 item.
- Tax Calculations: Determining the amount of sales tax or income tax owed.
- Financial Analysis: Evaluating investment returns, interest rates, and loan repayments.
- Data Analysis: Presenting data in a more easily understandable format using percentages, such as market share or survey results.
- Scientific Research: Representing experimental results and statistical significance.
- Grade Calculation: Converting raw scores to percentages.
Addressing Common Misconceptions
Several misconceptions can hinder accurate percentage calculations. Let's address some of the most common:
- Confusing Part and Whole: It's crucial to identify the correct "part" and "whole" values in the problem. Incorrectly identifying these can lead to inaccurate results.
- Improper Rounding: Rounding off numbers too early in the calculation can result in significant errors. It's best to retain several decimal places until the final answer.
- Misunderstanding Percentage Increase/Decrease: A percentage increase or decrease is calculated based on the original value, not the new value.
Expanding on Percentage Concepts
Beyond the basic calculations, several related concepts build upon the foundation of percentages:
- Percentage Change: This measures the change between two values as a percentage of the original value. The formula is: [(New Value - Original Value) / Original Value] * 100.
- Percentage Point: This represents the difference between two percentages. For example, a change from 10% to 15% is a 5 percentage point increase.
- Compound Interest: Interest calculated on the principal amount plus accumulated interest from previous periods.
- Percentage Yield: In finance, this describes the return on an investment relative to the amount invested.
Advanced Percentage Problems and Solutions
Let's explore some more complex problems that involve percentages:
Problem 1: A store offers a 15% discount on an item originally priced at $80. What is the final price after the discount?
- Solution: First, calculate the discount amount: 15% of $80 = (15/100) * $80 = $12
- Subtract the discount from the original price: $80 - $12 = $68
- The final price after the discount is $68.
Problem 2: After a 10% increase, a quantity becomes 110. What was the original quantity?
- Solution: Let 'x' be the original quantity. A 10% increase means it becomes 1.1x (100% + 10% = 110%). So, 1.1x = 110 x = 110 / 1.1 x = 100
- The original quantity was 100.
Problem 3: If 20% of a number is 30, what is the number?
- Solution: Let 'x' be the number.
- 20% of x = 30
- 0.2x = 30
- x = 30 / 0.2
- x = 150
- The number is 150.
Conclusion
Mastering percentage calculations is a valuable skill that extends far beyond the classroom. From everyday shopping to complex financial analysis, the ability to accurately calculate and interpret percentages is essential for informed decision-making. By understanding the fundamental formula, exploring different calculation methods, and addressing common misconceptions, you can confidently tackle a wide range of percentage problems and apply this knowledge to various aspects of your life. Remember to practice regularly to solidify your understanding and build your proficiency. The more you practice, the more comfortable and efficient you will become with percentage calculations.
Latest Posts
Latest Posts
-
How Much Is 50000 Hawaiian Miles Worth
May 11, 2025
-
How Many Minutes In 8 Days
May 11, 2025
-
Cuantos Dias Faltan Para El 28 De Marzo
May 11, 2025
-
Cuantos Metros Es Un Acre De Terreno
May 11, 2025
-
90 Days From August 1st 2024
May 11, 2025
Related Post
Thank you for visiting our website which covers about 7 Is What Percent Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.