7 Out Of 21 As A Percentage
Treneri
May 13, 2025 · 4 min read
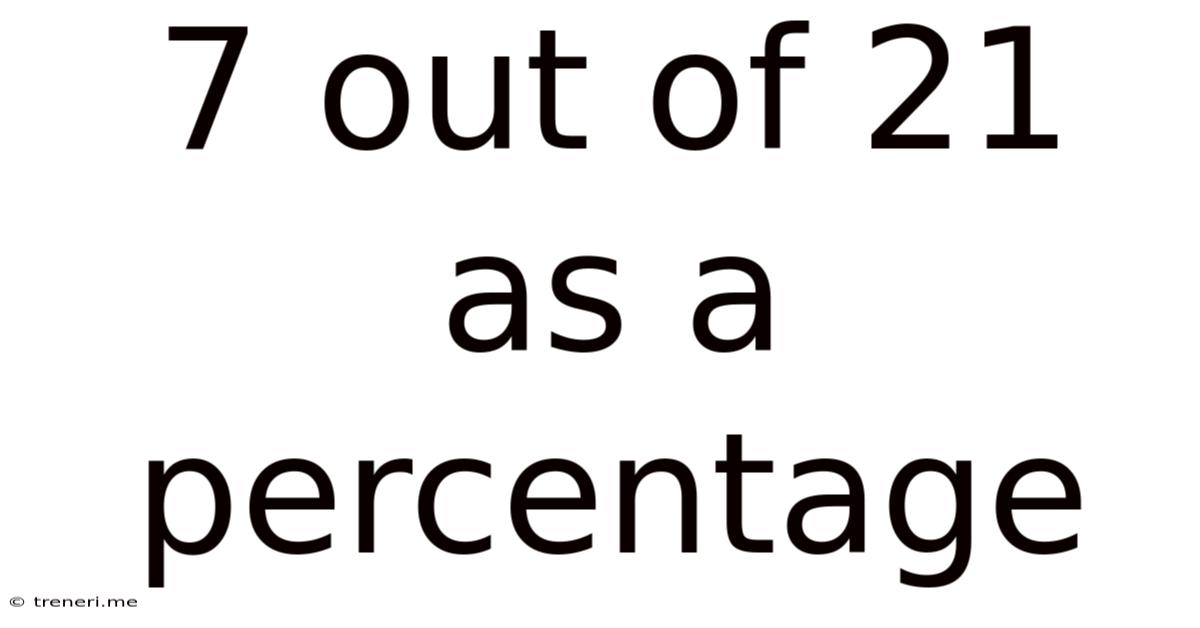
Table of Contents
7 Out of 21 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex statistical analysis. Understanding how to convert fractions into percentages is particularly crucial. This article will delve into the specific calculation of 7 out of 21 as a percentage, providing a step-by-step guide and exploring the broader context of percentage calculations. We'll also look at practical applications and related percentage problems.
Understanding Percentages
Before diving into the calculation, let's establish a firm understanding of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to ½ or 0.5 in decimal form.
Calculating 7 Out of 21 as a Percentage
To determine the percentage equivalent of 7 out of 21, we follow these straightforward steps:
Step 1: Express the values as a fraction.
7 out of 21 can be written as the fraction 7/21.
Step 2: Simplify the fraction (if possible).
Both the numerator (7) and the denominator (21) are divisible by 7. Simplifying the fraction gives us 1/3.
Step 3: Convert the fraction to a decimal.
To convert the fraction 1/3 to a decimal, divide the numerator (1) by the denominator (3):
1 ÷ 3 ≈ 0.3333... (This is a recurring decimal)
Step 4: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.3333... × 100 ≈ 33.33%
Therefore, 7 out of 21 is approximately 33.33%.
Rounding Percentages
Note that in the above calculation, we encountered a recurring decimal. In practical applications, it's often necessary to round percentages to a specific number of decimal places. The level of precision required depends on the context. For example:
- For general purposes: Rounding to one or two decimal places (33.33%) is usually sufficient.
- For financial calculations: Greater precision may be necessary, potentially rounding to more decimal places or even avoiding rounding altogether and working with the exact fraction.
Alternative Calculation Method: Using Proportions
Another approach to solving this problem involves using proportions. We can set up a proportion to find the equivalent percentage:
7/21 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x,' we cross-multiply:
21x = 700
x = 700/21
x ≈ 33.33
This method confirms our previous calculation.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins. Understanding percentage change is crucial for tracking investment performance and budgeting effectively.
-
Statistics: Percentages are essential for representing data in charts and graphs, interpreting survey results, and expressing probabilities. Analyzing data using percentages enables meaningful comparisons and insights.
-
Science: Percentage yields in chemical reactions, error margins in experiments, and expressing concentrations of solutions.
-
Everyday Life: Calculating tips in restaurants, understanding sale discounts in stores, and interpreting nutritional information on food labels.
Related Percentage Problems & Calculations
Let's explore some related percentage problems to further solidify the understanding of percentage calculations:
1. Finding a Percentage of a Number:
What is 30% of 150?
To calculate this, multiply 150 by 0.30 (the decimal equivalent of 30%):
150 × 0.30 = 45
2. Finding the Percentage Increase or Decrease:
A product initially priced at $100 is now priced at $120. What is the percentage increase?
First, calculate the difference: $120 - $100 = $20
Then, divide the difference by the original price and multiply by 100:
($20 / $100) × 100 = 20%
The price has increased by 20%.
3. Finding the Original Value:
After a 15% discount, a product costs $85. What was the original price?
Let 'x' be the original price. A 15% discount means the final price is 85% of the original price:
0.85x = 85
x = 85 / 0.85
x = 100
The original price was $100.
Advanced Percentage Concepts
For those seeking a deeper understanding, here are some more advanced percentage-related concepts:
-
Compound interest: Interest calculated on both the principal amount and accumulated interest.
-
Percentage points: The difference between two percentages. For example, a change from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Weighted averages: Calculating an average where different values have different weights or importance.
Conclusion
Mastering percentage calculations is a valuable skill with broad applications. This article has provided a comprehensive guide to calculating 7 out of 21 as a percentage, along with various practical examples and related percentage problems. By understanding the fundamental principles and practicing different types of calculations, you'll be well-equipped to tackle percentage-related problems with confidence in various academic and professional contexts. Remember to always check your work and consider the context when rounding percentages to ensure accuracy and clarity.
Latest Posts
Latest Posts
-
How Many Cubic Feet In 20 Gallons
May 13, 2025
-
How Much Ml Is Half A Cup
May 13, 2025
-
1981 Al 2024 Cuantos Anos Son
May 13, 2025
-
104 Km Is Equal To How Many Meters
May 13, 2025
-
5 Pies 4 Pulgadas A Metros
May 13, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.