7 Out Of 24 As A Percentage
Treneri
May 14, 2025 · 5 min read
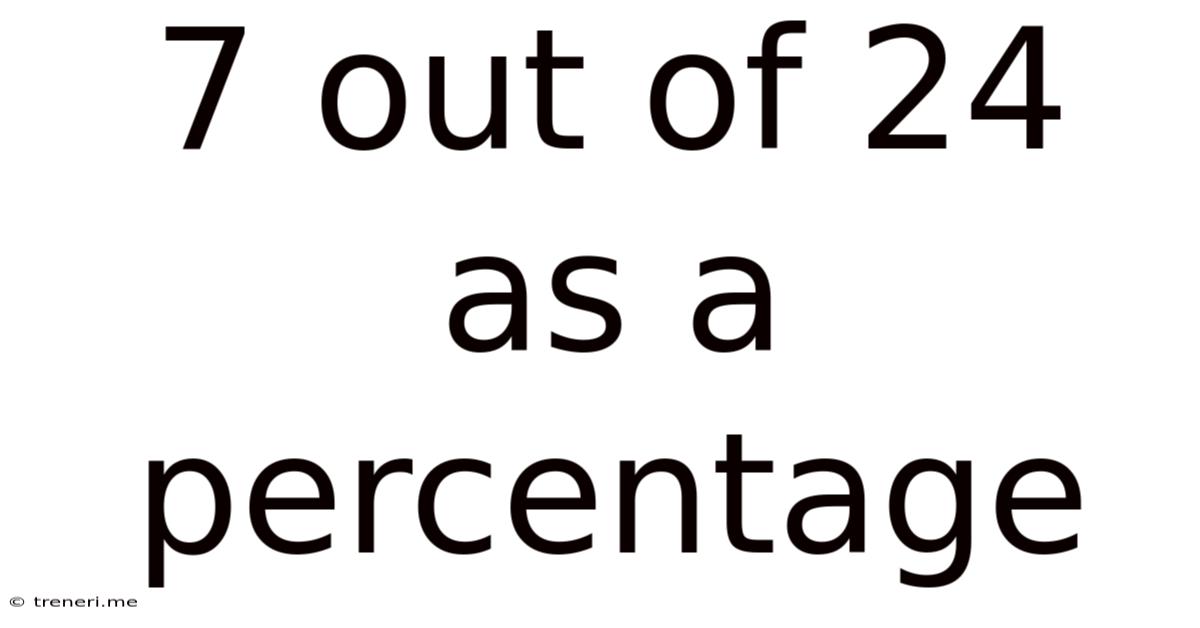
Table of Contents
7 Out of 24 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and communicating effectively. This comprehensive guide will delve into the calculation of "7 out of 24 as a percentage," providing not only the solution but also a detailed explanation of the underlying principles and various methods to tackle similar problems. We will explore different approaches, offering flexibility for diverse skill levels and problem-solving preferences.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the specific calculation, let's establish a solid foundation in the relationships between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fraction: A fraction expresses a part of a whole as a ratio of two numbers – a numerator (top number) and a denominator (bottom number). In our case, "7 out of 24" is represented as the fraction 7/24.
-
Decimal: A decimal expresses a part of a whole using a base-ten system. Decimals are essentially fractions where the denominator is a power of 10 (e.g., 10, 100, 1000).
-
Percentage: A percentage expresses a part of a whole as a fraction of 100. The symbol "%" denotes "per cent" or "out of 100."
The core relationship is that fractions, decimals, and percentages are all interchangeable. We can convert between them seamlessly using simple mathematical operations.
Method 1: Direct Conversion from Fraction to Percentage
The most straightforward method to determine "7 out of 24 as a percentage" involves directly converting the fraction 7/24 into a percentage. This involves two steps:
-
Convert the fraction to a decimal: Divide the numerator (7) by the denominator (24). This yields a decimal value:
7 ÷ 24 ≈ 0.2916666667
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
0.2916666667 × 100 ≈ 29.17%
Therefore, 7 out of 24 is approximately 29.17%. We round the decimal to two decimal places for practical purposes. The slight rounding error means the result isn't perfectly precise, but it's accurate enough for most applications.
Method 2: Using Proportions
Another approach leverages the concept of proportions. We can set up a proportion to solve for the percentage:
-
Let 'x' represent the percentage we want to find.
-
We can set up the proportion: 7/24 = x/100
To solve for 'x', we cross-multiply:
-
24x = 700
-
x = 700/24
-
x ≈ 29.17
Again, we arrive at approximately 29.17%. This method highlights the underlying proportional relationship between the fraction and the percentage.
Method 3: Understanding Percentage as a Ratio Out of 100
This method emphasizes the definition of percentage – a ratio out of 100. We need to find what part of 100 is equivalent to 7/24. We can express this as:
(7/24) * 100 = ?
Calculating this gives us:
29.166666... %
Rounding this to two decimal places, we get 29.17%. This method reinforces the fundamental concept of percentages as representing parts of a hundred.
Practical Applications and Real-World Examples
The ability to calculate percentages like "7 out of 24" has numerous practical applications:
-
Academic Performance: If a student answered 7 out of 24 questions correctly on a test, their score is approximately 29.17%.
-
Sales and Marketing: If a company made 7 sales out of 24 potential leads, their conversion rate is roughly 29.17%.
-
Financial Analysis: If an investment portfolio grew by 7 points out of a total of 24 points, the growth percentage is approximately 29.17%.
-
Survey Results: If 7 out of 24 respondents answered "yes" to a particular question in a survey, the positive response rate is around 29.17%.
Beyond the Basics: Handling Larger Numbers and Complex Scenarios
While the example of 7 out of 24 is relatively simple, the same principles extend to more complex scenarios involving larger numbers or multiple percentages. For instance:
-
Calculating multiple percentages: Imagine you need to calculate the percentage of multiple components contributing to a whole. You can apply the same fractional to percentage conversion method individually for each component and then sum the results.
-
Dealing with larger numbers: The method remains the same, regardless of the size of the numbers. You can use a calculator or spreadsheet software to handle larger computations easily.
-
Working with decimals in the numerator and denominator: If the numerator or denominator contains decimals, you can convert them to whole numbers by multiplying both by a suitable power of 10 before proceeding with the calculation.
Using Technology for Efficient Calculations
For more complex percentage calculations or when dealing with large datasets, using technology can significantly improve efficiency:
-
Spreadsheets: Spreadsheet software like Microsoft Excel or Google Sheets offer built-in functions for percentage calculations. You can directly input the fraction or the values and the software will automatically calculate the percentage.
-
Calculators: Scientific or graphing calculators typically have a percentage function that simplifies the conversion process.
Conclusion: Mastering Percentage Calculations for Data Interpretation and Decision-Making
The ability to convert fractions to percentages is a valuable skill that empowers you to interpret data, make informed decisions, and communicate effectively. Understanding the fundamental principles and applying the various methods discussed in this guide – direct conversion, proportions, and the ratio-out-of-100 approach – provides the flexibility to tackle a wide range of percentage calculations. Remember, practice is key to mastering this skill, and using technology can enhance efficiency for more complex scenarios. The calculation of "7 out of 24 as a percentage," while a seemingly simple problem, serves as a robust illustration of the broader principles of percentage calculation and their widespread applicability. By grasping these concepts thoroughly, you can confidently navigate a multitude of situations requiring percentage calculations, ultimately enhancing your analytical and problem-solving abilities.
Latest Posts
Latest Posts
-
1 Micro Drop Is Equal To
May 14, 2025
-
Greatest Common Factor Of 20 And 6
May 14, 2025
-
How Many Ounces Is 68 G
May 14, 2025
-
Cuanto Es 42 Onzas En Litros
May 14, 2025
-
Cuantas Quincenas Tiene El Ano 2024
May 14, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 24 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.