70 Is 1/10 Of What Number
Treneri
May 12, 2025 · 5 min read
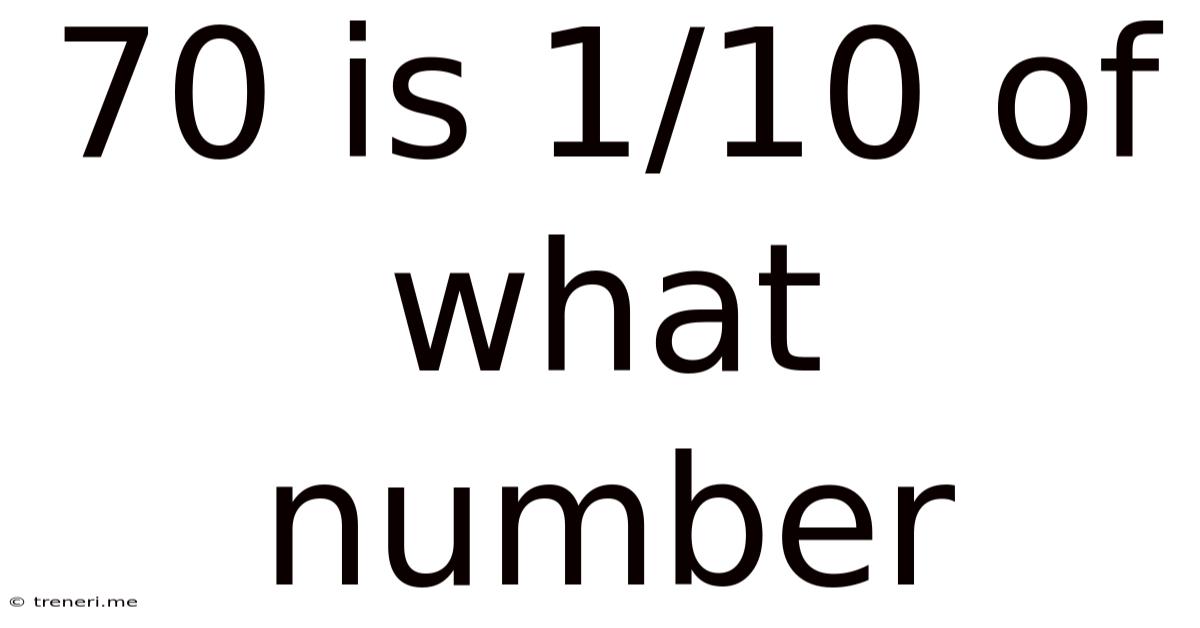
Table of Contents
70 is 1/10 of What Number? Unlocking the Power of Fractions and Algebra
Have you ever encountered a math problem that seems deceptively simple at first glance, yet holds a deeper mathematical significance? The question, "70 is 1/10 of what number?" is one such example. While the solution might seem immediately apparent to some, exploring this problem allows us to delve into the fundamental concepts of fractions, algebra, and problem-solving strategies. This article will not only provide the solution but also unpack the underlying mathematical principles and explore various methods to tackle similar problems. We'll even touch upon real-world applications to demonstrate the practical utility of understanding such concepts.
Understanding the Problem: Deconstructing the Question
The core of the problem lies in translating the word problem into a mathematical equation. The phrase "70 is 1/10 of what number" can be broken down as follows:
- "70 is": This translates directly to "70 =".
- "1/10 of": This represents multiplication: "× (1/10)".
- "what number": This is our unknown variable, which we'll represent as 'x'.
Therefore, the complete mathematical equation becomes:
70 = (1/10) * x
Method 1: Solving Using Multiplication
The most straightforward approach to solving this equation is to isolate the variable 'x'. To do this, we need to eliminate the fraction (1/10) from the right-hand side of the equation. Since multiplication and division are inverse operations, we can achieve this by multiplying both sides of the equation by the reciprocal of (1/10), which is 10:
70 * 10 = (1/10) * x * 10
This simplifies to:
700 = x
Therefore, 70 is 1/10 of 700.
Method 2: Solving Using Division
Another way to approach this problem is to think of it in terms of division. If 70 represents one-tenth of a number, then that number must be ten times larger than 70. This leads us directly to the solution:
70 / (1/10) = x
Remember that dividing by a fraction is the same as multiplying by its reciprocal:
70 * 10 = x
700 = x
Again, we arrive at the same solution: 70 is 1/10 of 700.
Method 3: Visualizing the Problem
For a more intuitive understanding, let's visualize the problem. Imagine a bar representing the whole number (x). If 70 represents 1/10 of this bar, then the entire bar must be ten times longer. This visual representation reinforces the concept of multiplying 70 by 10 to find the total value.
Expanding the Concept: Working with Different Fractions
The fundamental principles applied to this problem can be extended to solve similar problems involving different fractions. For example, consider the problem: "35 is 1/5 of what number?" Following the same steps:
- Translate to an equation: 35 = (1/5) * x
- Multiply both sides by the reciprocal of (1/5): 35 * 5 = x
- Solve for x: 175 = x
Therefore, 35 is 1/5 of 175.
Let's try another example: "24 is 2/3 of what number?" This problem requires a slightly different approach:
- Translate to an equation: 24 = (2/3) * x
- Multiply both sides by the reciprocal of (2/3): 24 * (3/2) = x
- Simplify and solve for x: (24 * 3) / 2 = x => 72 / 2 = x => 36 = x
Therefore, 24 is 2/3 of 36.
Real-World Applications: Where Fractions Matter
Understanding how to solve problems involving fractions isn't just a matter of academic exercise; it has widespread real-world applications. Consider the following scenarios:
- Sales and Discounts: If a store advertises a 10% discount, and the discounted price is $70, the original price can be calculated using the same principles. ($70 is 9/10 of the original price).
- Financial Calculations: Interest calculations, percentage increases or decreases, and many other financial computations involve fractional relationships.
- Measurement and Scaling: Scaling recipes, blueprints, or maps often relies on understanding proportional relationships expressed through fractions.
- Data Analysis: Interpreting data often requires calculating percentages and proportions, which utilize fractional concepts.
Mastering Fractions: A Key to Mathematical Proficiency
The ability to confidently work with fractions and solve related problems is a cornerstone of mathematical proficiency. It lays the foundation for more advanced concepts in algebra, calculus, and other branches of mathematics. By understanding the underlying principles, you equip yourself with the tools to tackle increasingly complex problems and apply these concepts to numerous real-world situations. The simple problem of "70 is 1/10 of what number?" serves as a perfect introduction to these essential mathematical skills.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, we can extend this discussion to include:
- Percentage Problems: Understanding the relationship between fractions and percentages is crucial. The problem "70 is 10% of what number?" is essentially the same problem, highlighting the interchangeable nature of these concepts.
- Algebraic Manipulation: More complex problems may require more sophisticated algebraic manipulation to isolate the unknown variable. Practice with these techniques will improve your problem-solving abilities.
- Ratio and Proportion: Understanding ratios and proportions provides another lens through which to view these types of problems. Expressing the problem as a ratio (70:x = 1:10) can lead to an alternative solution method using cross-multiplication.
This article aims to empower you with a comprehensive understanding of the seemingly simple problem, "70 is 1/10 of what number?" By exploring different solution methods, visualizing the problem, and examining real-world applications, we have showcased the practical significance of mastering fundamental mathematical concepts. This knowledge serves as a strong foundation for tackling more advanced mathematical challenges and opens doors to a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
Cuantas Libras Hay En Un Galon
May 12, 2025
-
How To Calculate Molarity From Absorbance
May 12, 2025
-
100k Is Equal To 1 Million
May 12, 2025
-
4 1 3 As A Fraction
May 12, 2025
-
What Is 62 An Hour Annually
May 12, 2025
Related Post
Thank you for visiting our website which covers about 70 Is 1/10 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.