740 Divided By 20 With Remainder
Treneri
May 11, 2025 · 5 min read
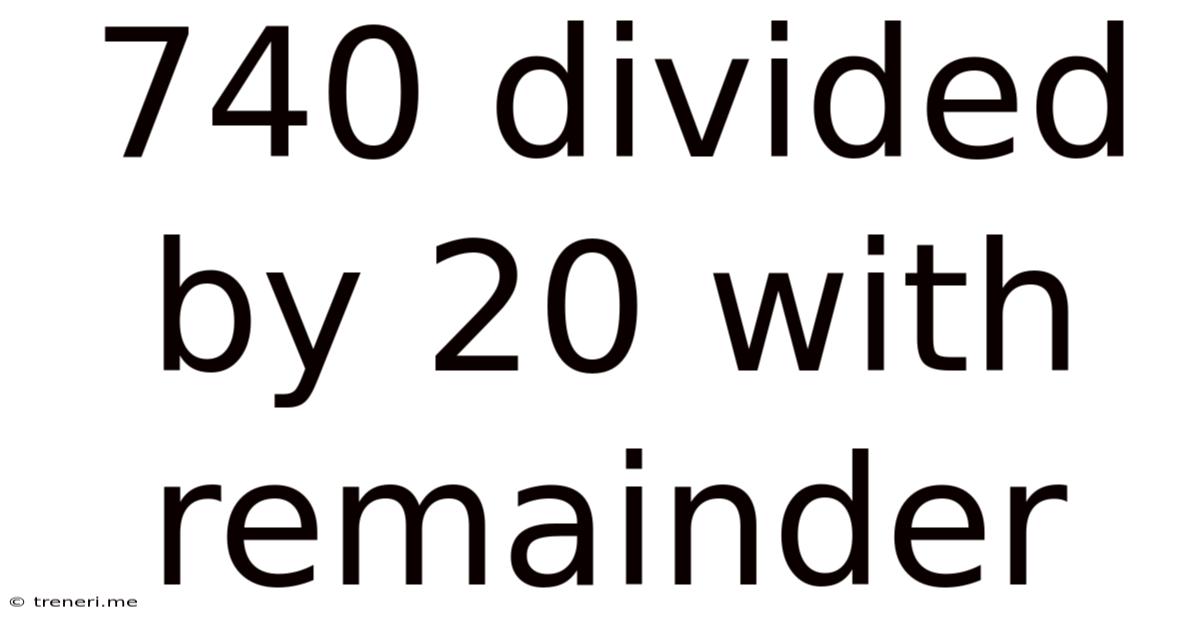
Table of Contents
740 Divided by 20 with Remainder: A Deep Dive into Division
Dividing 740 by 20 might seem like a simple arithmetic problem, but it provides a fantastic opportunity to explore various mathematical concepts and techniques. This article will delve deep into this seemingly straightforward calculation, exploring different approaches, examining the concept of remainders, and highlighting the practical applications of this fundamental operation. We'll go beyond just finding the answer and uncover the underlying mathematical principles that govern division.
Understanding Division: Beyond the Basics
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. When we divide 740 by 20, we're asking: "How many times does 20 fit into 740?" The answer to this question provides the quotient, while any amount left over represents the remainder.
The Long Division Method
The traditional method for solving this problem is long division. This method provides a step-by-step process for breaking down the division into manageable parts.
-
Set up the problem: Write 740 inside the long division symbol (÷) and 20 outside.
-
Divide the tens: 20 goes into 74 three times (3 x 20 = 60). Write the '3' above the '4' in 740.
-
Subtract: Subtract 60 from 74, leaving 14.
-
Bring down the ones: Bring down the '0' from 740, resulting in 140.
-
Divide the remaining number: 20 goes into 140 seven times (7 x 20 = 140). Write the '7' above the '0' in 740.
-
Subtract again: Subtract 140 from 140, leaving 0.
Therefore, 740 divided by 20 equals 37 with a remainder of 0.
Visual Representation:
37
20 | 740
-60
140
-140
0
Remainders: What They Mean and Why They Matter
The remainder is the amount left over after dividing a number as completely as possible. In the case of 740 divided by 20, the remainder is 0. This indicates that 20 divides 740 perfectly, leaving no leftover amount. However, remainders are not always 0. Let's consider a slightly different example.
Example with a Remainder: 745 Divided by 20
If we divide 745 by 20 using long division:
-
20 goes into 74 three times (3 x 20 = 60).
-
Subtracting 60 from 74 leaves 14.
-
Bringing down the 5 gives us 145.
-
20 goes into 145 seven times (7 x 20 = 140).
-
Subtracting 140 from 145 leaves a remainder of 5.
Therefore, 745 divided by 20 is 37 with a remainder of 5. This remainder signifies that 5 units are left over after dividing 745 into groups of 20.
Visual Representation:
37 R 5
20 | 745
-60
145
-140
5
Practical Applications of Division with Remainders
Understanding division with remainders has many practical applications in everyday life and various fields. Here are a few examples:
-
Sharing: Imagine you have 745 candies to distribute equally among 20 children. Each child would receive 37 candies, and you would have 5 candies left over.
-
Measurement: If you need to cut a 745cm long rope into 20 equal pieces, each piece would be 37cm long, with a 5cm piece remaining.
-
Scheduling: If you have a project requiring 745 hours of work to be completed over 20 weeks, each week would need approximately 37 hours of work, leaving 5 hours to allocate elsewhere.
-
Computer Science: Remainders are extensively used in computer algorithms and programming, particularly in tasks involving modular arithmetic and cryptography.
-
Engineering: Remainders appear in many engineering calculations related to resource allocation, material cutting, and component design.
Alternative Methods for Division
While long division is a standard method, other techniques can be used to solve division problems, especially when dealing with simpler numbers.
Repeated Subtraction
This method involves repeatedly subtracting the divisor (20) from the dividend (740) until the result is less than the divisor. The number of times you subtract represents the quotient, and the remaining amount is the remainder.
740 - 20 = 720
720 - 20 = 700
...and so on until you reach a number less than 20.
This method, while conceptually straightforward, can become tedious for larger numbers.
Multiplication and Estimation
You can estimate the quotient by using multiplication. Since 20 x 30 = 600 and 20 x 40 = 800, we know the quotient lies between 30 and 40. Further refinement through trial and error can lead to the exact quotient.
Exploring the Concept of Divisibility
The concept of divisibility is crucial when understanding remainders. A number is divisible by another if it can be divided by that number without leaving a remainder. In our initial problem, 740 is divisible by 20 because the remainder is 0. However, 745 is not divisible by 20 because there is a remainder of 5.
Understanding divisibility rules can help determine whether a number is divisible by another without performing the full division. For example, a number is divisible by 20 if it's divisible by both 4 and 5 (because 20 = 4 x 5).
Advanced Concepts: Modular Arithmetic
The concept of remainders forms the basis of modular arithmetic, a branch of number theory that deals with arithmetic operations within a given range (the modulus). In modular arithmetic, we're often interested in the remainder rather than the quotient. For instance, 745 modulo 20 (written as 745 mod 20) equals 5, which represents the remainder when 745 is divided by 20. Modular arithmetic has applications in cryptography, computer science, and various other fields.
Conclusion: The Power of Simple Division
Although seemingly simple, the problem of dividing 740 by 20 unlocks a wide range of mathematical concepts and practical applications. From understanding long division and remainders to exploring divisibility rules and modular arithmetic, this seemingly basic calculation illuminates the rich tapestry of mathematical principles. Mastering division, with its nuances and applications, forms a cornerstone for more advanced mathematical studies and practical problem-solving in diverse fields. The ability to understand and apply these concepts ensures a strong foundation for tackling more complex calculations and real-world challenges.
Latest Posts
Latest Posts
-
Can You Tan In 3 Uv
May 12, 2025
-
What Is 20 Stone In Lbs
May 12, 2025
-
Cuantos Dias Faltan Para El 21 De Octubre
May 12, 2025
-
Cuantas Son 116 Libras En Kilogramos
May 12, 2025
-
How Many Days Until June 14 Countdown
May 12, 2025
Related Post
Thank you for visiting our website which covers about 740 Divided By 20 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.