8 Out Of 21 As A Percentage
Treneri
May 13, 2025 · 5 min read
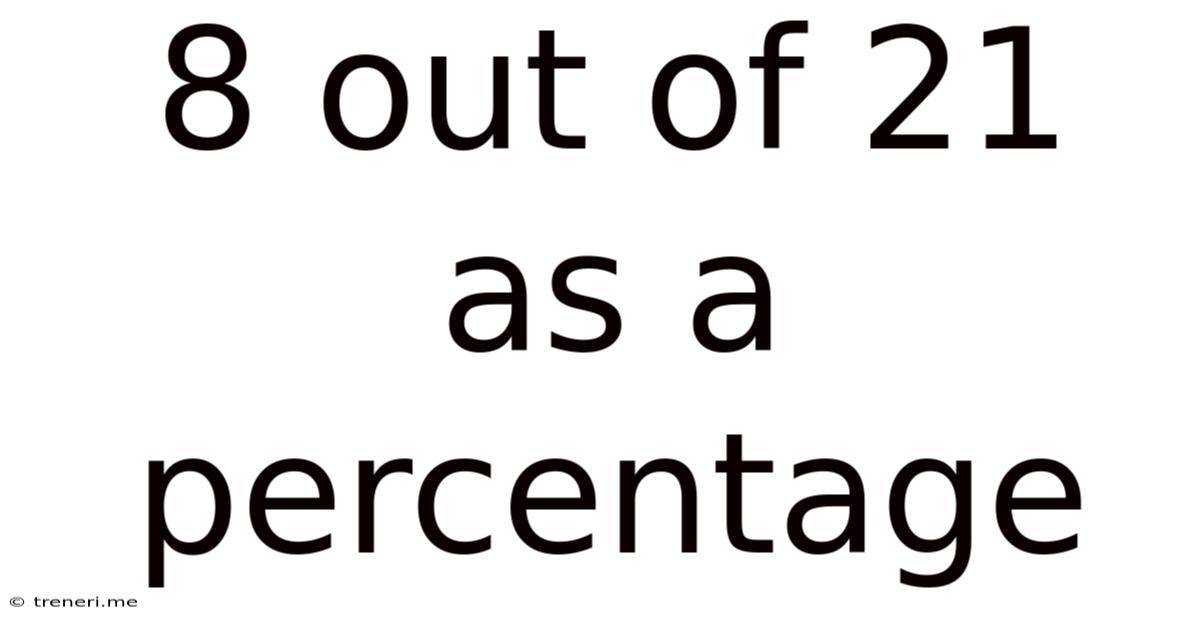
Table of Contents
8 Out of 21 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday finances to advanced statistical analysis. Understanding how to convert fractions and ratios into percentages is crucial for making informed decisions and interpreting data effectively. This article delves into the specific calculation of 8 out of 21 as a percentage, explaining the process step-by-step and exploring related concepts to enhance your understanding of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, when we say "x percent," we mean x out of 100, or x/100. This representation is incredibly useful because it provides a standardized way to compare different proportions.
Calculating 8 Out of 21 as a Percentage: The Step-by-Step Process
To find the percentage that 8 represents out of 21, we follow these straightforward steps:
Step 1: Set up the Fraction:
First, express the ratio as a fraction: 8/21. This fraction represents the part (8) relative to the whole (21).
Step 2: Convert the Fraction to a Decimal:
Divide the numerator (8) by the denominator (21):
8 ÷ 21 ≈ 0.380952
Step 3: Convert the Decimal to a Percentage:
Multiply the decimal by 100:
0.380952 × 100 ≈ 38.0952%
Step 4: Round to the Desired Precision:
Depending on the context and required level of accuracy, you can round the percentage. Common rounding practices include rounding to the nearest whole number, tenth, or hundredth. For example:
- Rounded to the nearest whole number: 38%
- Rounded to one decimal place: 38.1%
- Rounded to two decimal places: 38.10%
Therefore, 8 out of 21 is approximately 38.10%.
Different Methods for Calculating Percentages
While the above method is the most straightforward, there are alternative approaches to calculate percentages, particularly useful for different scenarios or when using different tools:
Method 1: Using a Calculator:
Most calculators have a percentage function. You can directly input 8/21 and press the percentage button (%) to obtain the result.
Method 2: Using a Spreadsheet Program (like Excel or Google Sheets):
Spreadsheet programs offer built-in functions for percentage calculations. For instance, in Excel or Google Sheets, you can use the formula =8/21*100 to directly calculate the percentage.
Method 3: Using Proportions:
You can also solve this using proportions. Set up the proportion:
8/21 = x/100
Cross-multiply and solve for x:
21x = 800 x = 800/21 ≈ 38.0952
This confirms our previous calculation.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various aspects of daily life and professional settings:
1. Finance:
- Calculating interest rates: Interest earned on savings accounts or paid on loans is expressed as a percentage.
- Determining discounts: Sales and discounts are often advertised as percentage reductions.
- Analyzing financial statements: Financial ratios and key performance indicators (KPIs) are often expressed as percentages to facilitate comparisons.
- Calculating taxes: Taxes are typically calculated as a percentage of income or the value of goods and services.
2. Statistics and Data Analysis:
- Representing data: Percentages are used to represent proportions and frequencies in data sets, making it easier to visualize and interpret trends.
- Calculating probabilities: Probabilities are often expressed as percentages.
- Analyzing survey results: Survey data is often presented in terms of percentages to show the distribution of responses.
3. Education:
- Grading systems: Grades are often expressed as percentages.
- Calculating test scores: Test scores are often represented as percentages of the total possible points.
4. Science:
- Expressing concentrations: Concentrations of solutions are often expressed as percentages.
- Analyzing experimental data: Percentage change is a common metric in scientific experiments.
5. Everyday Life:
- Calculating tips: Tips in restaurants are usually calculated as a percentage of the bill.
- Understanding sales tax: Sales tax is a percentage added to the price of goods and services.
Common Mistakes to Avoid When Calculating Percentages
While percentage calculations are relatively straightforward, some common errors can lead to inaccurate results:
- Incorrect order of operations: Ensure that you perform the division before multiplying by 100.
- Rounding errors: Be mindful of rounding errors, especially when dealing with multiple percentage calculations. Carry out calculations to several decimal places before rounding the final answer.
- Confusing percentages with decimal values: Remember that a percentage is a fraction of 100, not a simple decimal.
Advanced Percentage Calculations: Beyond the Basics
While calculating 8 out of 21 as a percentage is a fundamental application, understanding percentages extends to more complex scenarios:
1. Percentage Change:
Calculating percentage change involves comparing two values to determine the percentage increase or decrease. The formula is:
(New Value - Old Value) / Old Value * 100
2. Percentage Points:
Percentage points represent the difference between two percentages, not a percentage change. For example, if the unemployment rate increases from 5% to 7%, the increase is 2 percentage points, not a 40% increase.
3. Compound Percentages:
Compound percentages involve applying a percentage to a value repeatedly over time, considering the accumulated effect of previous applications.
4. Weighted Averages:
Weighted averages use percentages to assign different weights to different values, reflecting their relative importance.
Conclusion
Calculating 8 out of 21 as a percentage, resulting in approximately 38.10%, is a simple yet crucial skill. Understanding this fundamental calculation, along with the broader concepts of percentages, decimal conversions, and various calculation methods, empowers individuals and professionals to interpret data effectively, make sound financial decisions, and excel in diverse fields. By mastering these techniques and avoiding common pitfalls, you will significantly enhance your analytical and problem-solving capabilities. Remember to practice regularly and apply these principles in real-world scenarios to solidify your understanding and improve your proficiency in percentage calculations.
Latest Posts
Latest Posts
-
363 Rounded To The Nearest Ten And Hundred
May 13, 2025
-
Tamanho De Sapato Eua X Brasil
May 13, 2025
-
How To Find Height Of Right Triangle
May 13, 2025
-
What Is The Size Of My Phone Screen
May 13, 2025
-
0 05 Rounded To The Nearest Tenth
May 13, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.