80 Out Of 120 As A Percentage
Treneri
May 14, 2025 · 5 min read
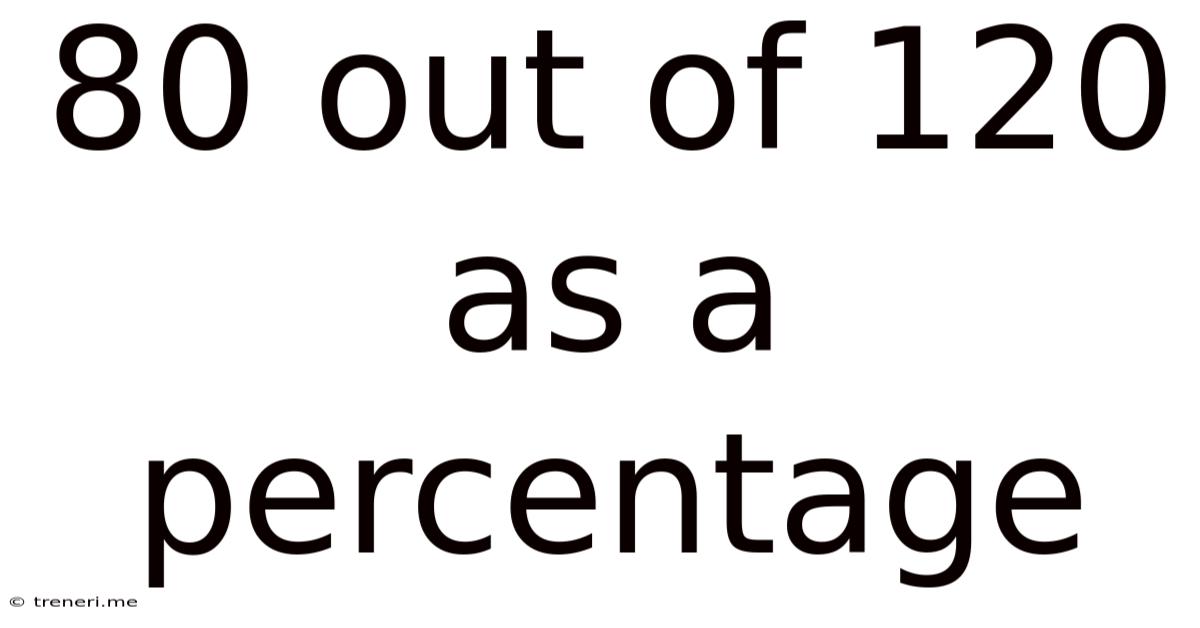
Table of Contents
80 out of 120 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and presenting information clearly. This comprehensive guide focuses on calculating 80 out of 120 as a percentage and explores the broader context of percentage calculations, equipping you with the knowledge to tackle similar problems confidently.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." The symbol "%" represents the percentage. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are used extensively to represent proportions, ratios, and rates of change. They provide a standardized way of comparing different quantities and understanding their relative sizes. This makes them invaluable tools in various applications, including:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates.
- Statistics: Representing data distributions, survey results, and probabilities.
- Science: Expressing concentrations, yields, and experimental errors.
- Everyday Life: Understanding sale discounts, tip calculations, and nutritional information.
Calculating 80 out of 120 as a Percentage
To calculate 80 out of 120 as a percentage, we follow these steps:
-
Express the given values as a fraction: The problem is presented as "80 out of 120," which can be written as the fraction 80/120.
-
Convert the fraction to a decimal: Divide the numerator (80) by the denominator (120): 80 ÷ 120 = 0.666666... (This is a repeating decimal).
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.666666... × 100 ≈ 66.67%.
Therefore, 80 out of 120 is approximately 66.67%. The slight rounding is necessary because the decimal is repeating.
Different Methods for Calculating Percentages
While the above method is straightforward, several other approaches can be used depending on the context and your comfort level with mathematical operations:
Method 1: Using Proportions:
This method leverages the concept of equivalent ratios. We set up a proportion:
x/100 = 80/120
To solve for 'x' (the percentage), we cross-multiply:
120x = 8000
x = 8000/120 = 66.67
Therefore, x ≈ 66.67%
Method 2: Using Simplification:
Before converting to a decimal, we can simplify the fraction 80/120. Both the numerator and the denominator are divisible by 40:
80/120 = (80 ÷ 40) / (120 ÷ 40) = 2/3
Now, converting 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667
Multiplying by 100 gives us approximately 66.67%.
Method 3: Using a Calculator:
Most calculators have a percentage function. Simply enter 80 ÷ 120 and then multiply the result by 100. The calculator will directly give you the percentage. This method is particularly useful for more complex percentage calculations.
Practical Applications of Percentage Calculations: Real-World Examples
Understanding percentage calculations is essential for navigating numerous real-world scenarios. Let's explore some practical examples:
1. Grade Calculations: Imagine a student scored 80 out of 120 marks in a test. As we've calculated, this represents 66.67%. This allows for easy comparison with other students' scores and provides a clear representation of their performance.
2. Sales Discounts: A store offers a 20% discount on an item originally priced at $120. To calculate the discount amount:
Discount = 20% of $120 = (20/100) * $120 = $24
The final price after the discount would be $120 - $24 = $96.
3. Interest Calculations: If you invest $1000 at an annual interest rate of 5%, the interest earned after one year would be:
Interest = 5% of $1000 = (5/100) * $1000 = $50
4. Tax Calculations: If the sales tax is 8% on a $60 purchase, the tax amount would be:
Tax = 8% of $60 = (8/100) * $60 = $4.80
The total cost including tax would be $60 + $4.80 = $64.80
5. Analyzing Survey Results: If 80 out of 120 respondents to a survey favored a particular product, this indicates a 66.67% approval rating.
Advanced Percentage Calculations: Beyond the Basics
While calculating 80 out of 120 as a percentage is a simple task, percentage calculations can become more complex. Here are a few scenarios requiring slightly more advanced techniques:
- Calculating Percentage Increase or Decrease: This involves determining the percentage change between two values. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
-
Calculating Percentage Points: Percentage points represent the arithmetic difference between two percentages, not the percentage change. For example, if interest rates increase from 2% to 5%, the increase is 3 percentage points, not a 150% increase.
-
Working with Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. Calculating compound interest requires more complex formulas.
-
Percentage of a Percentage: This involves finding a percentage of a percentage, often encountered in scenarios like calculating discounts on already discounted items.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill that extends far beyond academic settings. From managing personal finances to interpreting data and making informed business decisions, understanding how to work with percentages is essential. This guide provided a comprehensive overview of calculating 80 out of 120 as a percentage, explored different calculation methods, and showcased practical applications in various contexts. By understanding the principles and techniques outlined here, you can confidently tackle diverse percentage calculations in your personal and professional life. Remember to always double-check your work and consider the practical implications of your findings to ensure accuracy and meaningful interpretation.
Latest Posts
Latest Posts
-
How Many Hours In Four Days
May 14, 2025
-
Cuantos Dias Faltan Para 23 De Noviembre
May 14, 2025
-
What Is 8 To The Power Of 5
May 14, 2025
-
Cuanto Falta Para El 3 De Abril
May 14, 2025
-
What Is A 5 Out Of 6 Grade
May 14, 2025
Related Post
Thank you for visiting our website which covers about 80 Out Of 120 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.