800 Out Of 1000 As A Percentage
Treneri
May 12, 2025 · 5 min read
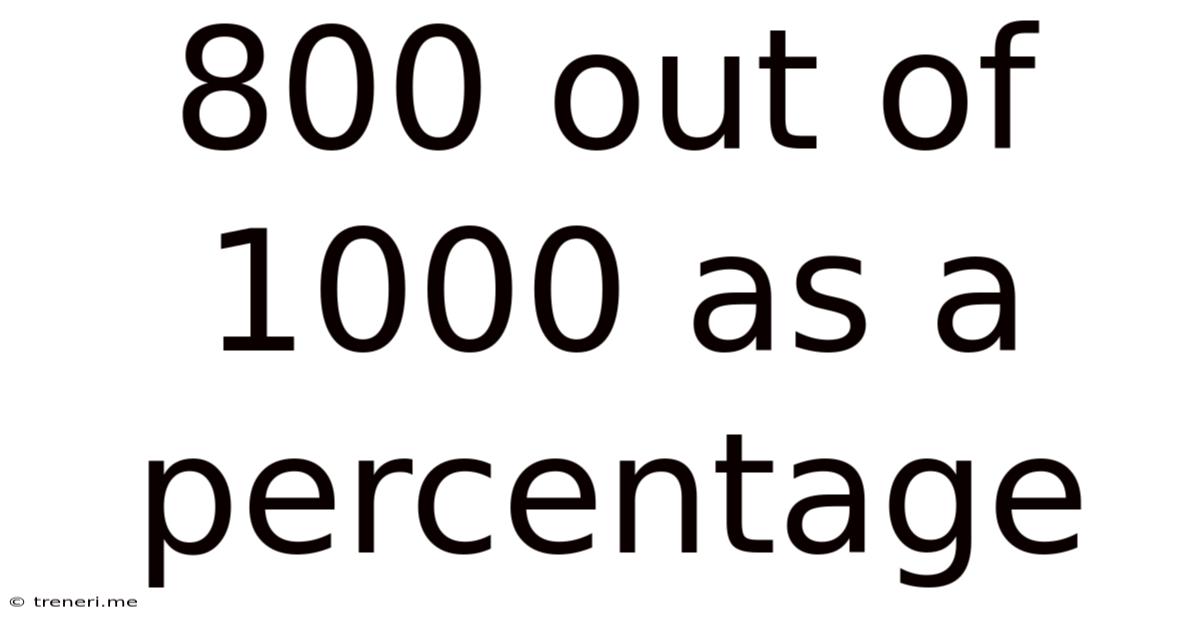
Table of Contents
800 out of 1000 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to express fractions as percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This article delves into the calculation of 800 out of 1000 as a percentage, exploring the methods involved, its real-world applications, and providing further insights into percentage calculations.
Understanding Percentages
Before we dive into the specific calculation, let's establish a firm understanding of what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5 in decimal form.
Percentages are widely used because they provide a standardized way to compare proportions and ratios regardless of the original quantities involved. This makes them invaluable for various applications, such as comparing test scores, analyzing market shares, calculating discounts, and understanding financial data.
Calculating 800 out of 1000 as a Percentage
There are two primary methods to calculate 800 out of 1000 as a percentage:
Method 1: Using the Fraction Method
This method involves representing the given numbers as a fraction and then converting the fraction into a percentage.
-
Express as a Fraction: The problem "800 out of 1000" can be written as the fraction 800/1000.
-
Simplify the Fraction (Optional): While not strictly necessary, simplifying the fraction can make the calculation easier. We can divide both the numerator (800) and the denominator (1000) by their greatest common divisor, which is 200. This simplifies the fraction to 4/5.
-
Convert to a Decimal: To convert the fraction to a decimal, divide the numerator by the denominator: 4 ÷ 5 = 0.8
-
Convert to a Percentage: To convert the decimal to a percentage, multiply the decimal by 100 and add the "%" symbol: 0.8 x 100 = 80%.
Therefore, 800 out of 1000 is 80%.
Method 2: Using the Percentage Formula
The percentage formula provides a direct way to calculate percentages:
Percentage = (Part / Whole) x 100
In this case:
- Part = 800
- Whole = 1000
Substituting these values into the formula:
Percentage = (800 / 1000) x 100 = 0.8 x 100 = 80%
Again, we arrive at the answer: 800 out of 1000 is 80%.
Real-World Applications of Percentage Calculations
The ability to calculate percentages has numerous practical applications across various domains:
1. Academic Performance:
-
Grade Calculation: Students frequently encounter percentage calculations when determining their final grades. For example, if a student scores 800 out of 1000 points on an exam, their score is 80%.
-
Test Scores: Standardized tests and assessments often report results as percentages, providing a clear indication of a student's performance relative to the total possible score.
2. Finance and Business:
-
Profit Margins: Businesses use percentage calculations to determine their profit margins, which represent the percentage of revenue remaining after deducting costs.
-
Interest Rates: Interest rates on loans and investments are expressed as percentages, indicating the amount charged or earned as a percentage of the principal amount.
-
Discounts and Sales: Retailers commonly advertise discounts as percentages, such as a "20% off" sale. Understanding percentage calculations is crucial for consumers to determine the actual price after the discount.
-
Tax Calculations: Taxes are often calculated as a percentage of income or the value of goods and services.
-
Investment Returns: Investors track their investment returns as percentages to assess the performance of their portfolio.
3. Science and Statistics:
-
Data Analysis: Percentage calculations are frequently used in scientific research and statistical analysis to represent proportions, probabilities, and changes in variables.
-
Experimental Results: Scientific experiments often involve measuring quantities and expressing the results as percentages to facilitate comparison and interpretation.
4. Everyday Life:
-
Shopping: Calculating discounts and sales tax involves percentage calculations.
-
Tipping: Calculating tips in restaurants often involves estimating a percentage of the total bill.
-
Surveys and Polls: Results from surveys and polls are frequently presented as percentages to represent the proportion of respondents who chose a particular option.
Beyond the Basics: Advanced Percentage Calculations
While calculating 800 out of 1000 is a straightforward example, understanding percentages extends to more complex scenarios. Here are some advanced concepts:
-
Percentage Increase/Decrease: Calculating the percentage change between two values involves determining the difference between the two values, dividing by the original value, and multiplying by 100.
-
Percentage Points: This term is crucial when comparing percentage changes. A change from 10% to 20% is a 10 percentage point increase, not a 100% increase.
-
Compounding Percentages: This concept deals with situations where percentages are applied repeatedly over time, such as compound interest.
-
Percentage of a Percentage: This involves calculating a percentage of a value that is already a percentage, requiring careful attention to the order of operations.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a valuable life skill applicable across numerous contexts. Understanding the different methods for calculating percentages, such as the fraction method and the percentage formula, empowers you to confidently tackle various numerical challenges. From everyday transactions to complex financial analysis, a strong grasp of percentage calculations is essential for making informed decisions and effectively interpreting data. By mastering these concepts, you enhance your ability to navigate the numerical world with greater accuracy and understanding. Remember to practice regularly and apply your knowledge in real-world scenarios to solidify your understanding and improve your proficiency.
Latest Posts
Latest Posts
-
Area Of A 16 Inch Pizza
May 13, 2025
-
How Much Is A 1 4 Lb Of Butter
May 13, 2025
-
25 Rounded To The Nearest 10
May 13, 2025
-
Convert Volume Flow To Mass Flow
May 13, 2025
-
How Much Is 200g In Oz
May 13, 2025
Related Post
Thank you for visiting our website which covers about 800 Out Of 1000 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.