82 Out Of 90 As A Percentage
Treneri
May 12, 2025 · 5 min read
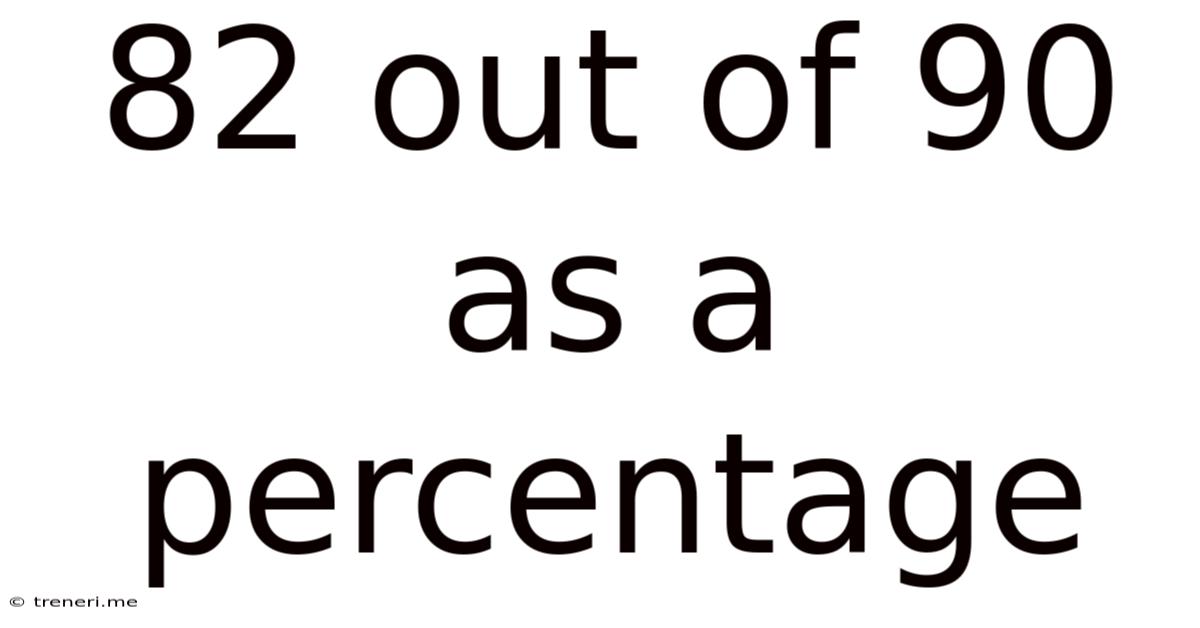
Table of Contents
82 out of 90 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial transactions and data analysis. Understanding how to convert fractions into percentages is crucial for interpreting data effectively and making informed decisions. This comprehensive guide focuses specifically on calculating 82 out of 90 as a percentage, providing a detailed explanation of the process, exploring different calculation methods, and highlighting practical applications. We'll also delve into the broader context of percentage calculations and their significance.
Understanding Percentages
A percentage represents a fraction of 100. It signifies a proportion or rate per hundred. The symbol "%" is used to denote a percentage. For instance, 50% signifies 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are versatile tools for expressing proportions and comparisons, making them essential in diverse fields.
Calculating 82 out of 90 as a Percentage: The Basic Method
The most straightforward method for converting a fraction to a percentage involves these steps:
-
Express the given numbers as a fraction: In this case, we have 82 out of 90, which is written as 82/90.
-
Convert the fraction to a decimal: To do this, divide the numerator (82) by the denominator (90). 82 ÷ 90 ≈ 0.9111
-
Multiply the decimal by 100: This converts the decimal to a percentage. 0.9111 x 100 = 91.11%
Therefore, 82 out of 90 is approximately 91.11%.
Alternative Calculation Methods
While the basic method is efficient, understanding alternative approaches can enhance your mathematical proficiency and provide different perspectives. Let's explore a couple of other methods:
Method 2: Using Proportions
This method leverages the concept of proportions to solve the problem. We can set up a proportion:
82/90 = x/100
Here, 'x' represents the percentage we need to find. To solve for 'x', cross-multiply:
90x = 8200
Then, divide both sides by 90:
x = 8200/90 ≈ 91.11
Therefore, x ≈ 91.11%, confirming the result obtained using the basic method.
Method 3: Simplifying the Fraction First
Before converting to a decimal, simplifying the fraction can sometimes make the calculations easier. While 82 and 90 don't have a large common factor, it's still a good practice to check: Both numbers are divisible by 2, resulting in the simplified fraction 41/45.
Now, dividing 41 by 45 gives approximately 0.9111. Multiplying by 100 gives the same result: 91.11%.
Significance and Applications of Percentage Calculations
The ability to calculate percentages efficiently is a valuable skill across various domains:
-
Academic Performance: Calculating grades, understanding class rankings, and assessing individual progress often involves percentage calculations. A score of 82 out of 90 on a test, as we've seen, translates to a strong grade.
-
Financial Management: Percentages are crucial for understanding interest rates, discounts, taxes, profit margins, and investment returns. Calculating percentage change is essential for tracking financial performance over time. For example, understanding percentage increase or decrease in investments is paramount for informed financial decisions.
-
Data Analysis and Interpretation: In statistics and data analysis, percentages are used extensively to present and interpret data effectively. They provide a clear and concise way to summarize and compare large datasets. For example, researchers use percentages to illustrate the percentage of respondents who chose a particular answer in a survey.
-
Retail and Sales: Discounts, markups, sales tax, and profit margins are all expressed as percentages. Retailers use percentages to calculate discounts, markups, and sales tax, ensuring accurate pricing and profitability.
-
Science and Engineering: Percentage calculations are used in various scientific and engineering applications, such as calculating efficiency, error rates, and concentrations. Understanding percentages is crucial in fields like chemistry and physics, where concentrations and reaction yields are frequently expressed as percentages.
Beyond the Calculation: Understanding the Context
While knowing how to calculate 82 out of 90 as a percentage is important, understanding the context is equally vital. The meaning of this percentage depends heavily on the situation. In a test, 91.11% might indicate excellent performance. However, in a manufacturing process, it could signal a significant defect rate, needing improvement.
Practical Examples: Applying Percentage Calculations
Let's illustrate the practicality of percentage calculations with real-world examples:
Example 1: Sales Performance:
A salesperson achieved 82 sales out of 90 potential clients. Their success rate is 91.11%. This high percentage indicates strong performance, potentially warranting recognition or incentives.
Example 2: Manufacturing Defects:
A factory produced 90 units of a product, with 82 units meeting quality standards. The defect rate is 8/90, or approximately 8.89%. This relatively low percentage might be acceptable, but monitoring and improvement efforts are still essential to maintain quality control.
Example 3: Survey Results:
In a survey of 90 participants, 82 indicated satisfaction with a particular product. The satisfaction rate is 91.11%, indicating high customer approval. This information can be used in marketing materials or to guide product development.
Conclusion
Calculating percentages is a fundamental mathematical skill with significant implications across various domains. This guide has demonstrated several methods for calculating 82 out of 90 as a percentage (approximately 91.11%), emphasizing its practical applications in diverse contexts. Beyond simply calculating the percentage, it is crucial to consider the context and interpret the result thoughtfully. Understanding percentages empowers you to analyze data, make informed decisions, and communicate information effectively in various fields, ultimately leading to better problem-solving and decision-making capabilities. Remember that accuracy and attention to detail are essential when working with percentages, particularly in situations where precision is paramount.
Latest Posts
Latest Posts
-
How Much Does 1 Ton Of Pea Gravel Cover
May 13, 2025
-
90 Days From Sep 16 2024
May 13, 2025
-
Number Of Days In 6 Months
May 13, 2025
-
3 Is What Percent Of 36
May 13, 2025
-
How To Find The Latus Rectum Of A Parabola
May 13, 2025
Related Post
Thank you for visiting our website which covers about 82 Out Of 90 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.