9 Is 30 Percent Of What Number
Treneri
May 14, 2025 · 4 min read
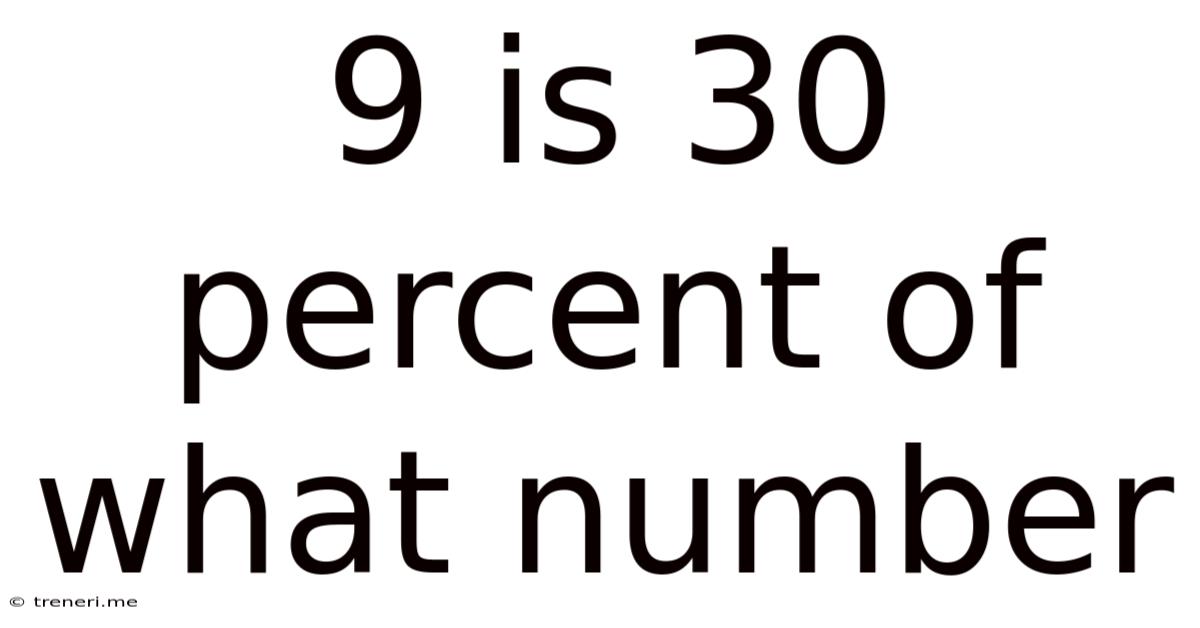
Table of Contents
9 is 30 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into the question, "9 is 30 percent of what number?", providing a step-by-step solution, exploring different methods of calculation, and expanding on the broader concept of percentage problems. We'll also cover practical examples and offer tips for solving similar problems efficiently.
Understanding Percentages
Before diving into the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote percentages. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Key Concepts
- Percentage: Represents a portion of a whole.
- Whole (or Base): The total amount or quantity.
- Part: The portion of the whole represented by the percentage.
In our problem, "9 is 30 percent of what number?", we know the part (9) and the percentage (30%). We need to find the whole (the unknown number).
Solving "9 is 30 Percent of What Number?"
There are several ways to approach this problem. Let's explore the most common methods:
Method 1: Using the Formula
The fundamental formula for percentage calculations is:
(Part / Whole) * 100% = Percentage
We can rearrange this formula to solve for the whole:
Whole = (Part / Percentage) * 100
Plugging in the values from our problem:
Whole = (9 / 30) * 100
Whole = 0.3 * 100
Whole = 30
Therefore, 9 is 30 percent of 30.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion as follows:
9 / x = 30 / 100
Where 'x' represents the unknown whole number. To solve for x, we can cross-multiply:
9 * 100 = 30 * x
900 = 30x
x = 900 / 30
x = 30
Again, we find that 9 is 30 percent of 30.
Method 3: Using Decimal Equivalents
We can convert the percentage to its decimal equivalent by dividing by 100. 30% is equivalent to 0.30 (or simply 0.3). Then, we can set up the equation:
0.3 * x = 9
Solving for x:
x = 9 / 0.3
x = 30
This method confirms that 9 is 30 percent of 30.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and professional settings. Here are a few examples:
1. Retail Discounts:
Imagine a store offers a 30% discount on an item originally priced at $30. Using our knowledge, we can easily calculate the discount amount:
Discount = 30% of $30 = 0.3 * $30 = $9
The final price after the discount would be $30 - $9 = $21.
2. Tax Calculations:
Sales tax is a percentage added to the price of goods and services. If the sales tax rate is 6%, and the price of an item is $50, the tax amount would be:
Tax = 6% of $50 = 0.06 * $50 = $3
The total cost including tax would be $50 + $3 = $53.
3. Grade Calculation:
In education, percentages are used to express grades and scores. If a student scored 27 out of 30 on a test, their percentage score would be:
(27 / 30) * 100% = 90%
4. Financial Analysis:
Percentage changes are essential for analyzing financial data, such as stock market performance, profit margins, and interest rates.
Expanding on Percentage Problems: More Complex Scenarios
While the initial problem was straightforward, percentage problems can become more complex. Consider these scenarios:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two values. For example, if a stock price rises from $10 to $12, the percentage increase is calculated as:
[(12-10)/10] * 100% = 20%. -
Calculating percentages of percentages: This can occur in situations with multiple discounts or compounded interest. For instance, a 10% discount followed by a 20% discount is not equivalent to a 30% discount.
-
Solving problems involving multiple unknowns: These problems often require the use of simultaneous equations or algebraic manipulation to find the solutions.
Tips for Solving Percentage Problems Efficiently
- Understand the problem: Clearly identify the known and unknown quantities.
- Choose the appropriate method: Select the method that best suits the problem's complexity.
- Double-check your calculations: Verify your results using a different method or by estimation.
- Practice regularly: Consistent practice will enhance your understanding and improve your speed and accuracy.
Conclusion
The question, "9 is 30 percent of what number?" serves as a foundational example demonstrating the importance of percentage calculations in numerous contexts. By mastering different solution methods and understanding the underlying concepts, you can confidently tackle various percentage problems encountered in daily life and professional endeavors. Remember to utilize the formulas, proportions, or decimal equivalents to arrive at accurate solutions and always double-check your work. The ability to solve percentage problems efficiently contributes to stronger analytical skills and improved problem-solving capabilities.
Latest Posts
Latest Posts
-
How Much Longer Until 4 Pm Today
May 14, 2025
-
Paying Mortgage Weekly Vs Monthly Calculator
May 14, 2025
-
What Is An Equivalent Fraction To 4 10
May 14, 2025
-
What Is 2 Percent Of 4000
May 14, 2025
-
Como Calcular El Interes Compuesto Diario
May 14, 2025
Related Post
Thank you for visiting our website which covers about 9 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.