9 Out Of 18 As A Percentage
Treneri
May 14, 2025 · 5 min read
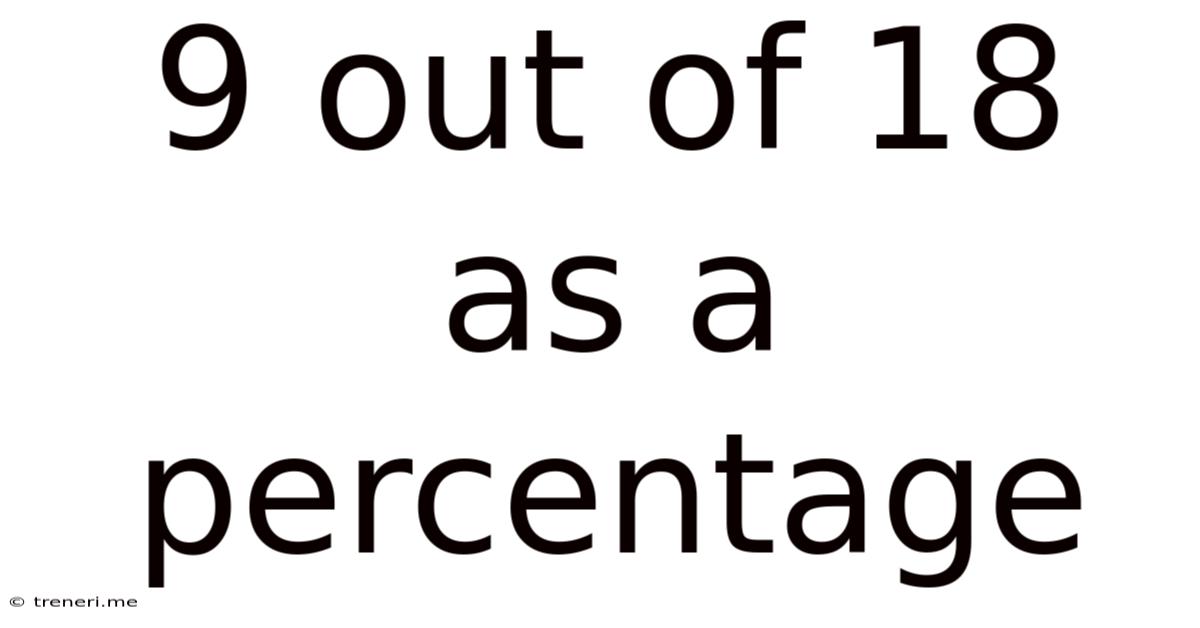
Table of Contents
9 out of 18 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in many aspects of life, from calculating discounts in a shop to analyzing data in a professional setting. This comprehensive guide will delve into how to calculate "9 out of 18 as a percentage," explaining the process in detail and exploring various applications. We'll also look at related concepts to solidify your understanding of percentage calculations.
Understanding the Basics of Percentages
Before we tackle the specific calculation, let's review the core concepts of percentages. A percentage is a fraction of 100, representing a proportion of a whole. The symbol "%" signifies a percentage.
For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. This signifies that 50% represents half of something.
Calculating 9 out of 18 as a Percentage
The problem "9 out of 18" can be expressed as a fraction: 9/18. To convert this fraction to a percentage, we need to follow these steps:
Step 1: Express the Fraction
The phrase "9 out of 18" is directly translated into the fraction 9/18.
Step 2: Simplify the Fraction (Optional but Recommended)
Simplifying the fraction often makes the calculation easier. In this case, both the numerator (9) and the denominator (18) are divisible by 9:
9 ÷ 9 = 1 18 ÷ 9 = 2
This simplifies the fraction to 1/2.
Step 3: Convert the Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator by the denominator:
1 ÷ 2 = 0.5
Step 4: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.5 x 100 = 50%
Therefore, 9 out of 18 is equal to 50%.
Alternative Calculation Method: Direct Percentage Calculation
While simplifying the fraction is generally helpful, you can also directly calculate the percentage without simplification:
Step 1: Express the fraction: 9/18
Step 2: Convert to a decimal: 9 ÷ 18 = 0.5
Step 3: Convert to a percentage: 0.5 x 100 = 50%
Both methods yield the same result: 50%. The choice of method depends on personal preference and the complexity of the fraction.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous everyday situations:
- Shopping: Calculating discounts, sales tax, and tips. If a shirt is 50% off, knowing how to calculate that discount is essential.
- Finance: Determining interest rates, loan repayments, and investment returns. Understanding percentage changes in your investment portfolio is vital for financial planning.
- Academics: Calculating grades, test scores, and overall performance. Your final grade is often expressed as a percentage of total points.
- Data Analysis: Interpreting data represented as percentages in graphs, charts, and reports. This is critical in fields like business, science, and social studies.
- Sports: Understanding batting averages, win percentages, and other statistical measures. Sports statistics are heavily reliant on percentage calculations.
- Cooking: Adjusting recipes based on percentage increases or decreases in ingredient quantities.
- Construction: Calculating material requirements based on percentages of total project needs.
Beyond the Basics: Working with More Complex Percentages
While 9 out of 18 is a relatively straightforward calculation, let's explore how to tackle more complex percentage problems:
Calculating Percentage Increase or Decrease
Percentage increase or decrease is commonly used to show changes over time. The formula is:
[(New Value - Old Value) / Old Value] x 100%
For example, if a stock price increases from $10 to $15, the percentage increase is:
[(15 - 10) / 10] x 100% = 50%
Similarly, if the price decreases from $15 to $10, the percentage decrease is:
[(10 - 15) / 15] x 100% = -33.33% (Note the negative sign indicating a decrease)
Finding the Original Value Given a Percentage
Sometimes, you know the percentage and the resulting value, but you need to find the original value. For example: A shirt is on sale for $25, representing a 20% discount. What was the original price?
Let 'x' represent the original price. The equation would be:
x - 0.20x = $25
Solving for x:
0.80x = $25
x = $25 / 0.80 = $31.25
The original price was $31.25.
Calculating Percentage of a Percentage
This involves finding a percentage of a percentage. For example, what is 10% of 20%?
First, convert the percentages to decimals: 0.10 and 0.20. Then multiply them:
0.10 x 0.20 = 0.02
Finally, convert the decimal back to a percentage: 0.02 x 100% = 2%
Therefore, 10% of 20% is 2%.
Troubleshooting Common Percentage Calculation Mistakes
Even simple percentage calculations can sometimes be tricky. Here are some common mistakes to avoid:
- Incorrect Order of Operations: When calculating percentage increases or decreases, ensure you subtract the values before dividing. Following the order of operations (PEMDAS/BODMAS) is crucial.
- Mixing Decimals and Percentages: Always convert percentages to decimals before performing calculations and then convert back to percentages at the end.
- Rounding Errors: Rounding intermediate results can lead to inaccuracies in the final answer. Try to retain as many decimal places as possible until the final calculation.
- Incorrect Interpretation of the Problem: Carefully read and understand the problem statement to ensure you are calculating the correct percentage.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a vital life skill. While the basic calculation, such as finding "9 out of 18 as a percentage," is relatively simple, the applications of percentage calculations extend far beyond this. By mastering the core concepts and avoiding common mistakes, you can confidently apply these skills in various aspects of your personal and professional life. Remember to practice regularly to reinforce your understanding and build your confidence in handling percentage-related problems. This comprehensive guide provides a solid foundation for tackling a wide range of percentage calculations, empowering you to approach numerical problems with greater accuracy and efficiency.
Latest Posts
Latest Posts
-
What Grade Is 15 Out Of 18
May 14, 2025
-
3 Hour 25 Min Marathon Pace
May 14, 2025
-
24 Is What Percent Of 800
May 14, 2025
-
How Many Calories Is In 1g Of Protein
May 14, 2025
-
5 535 Rounded To The Nearest Hundredth
May 14, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 18 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.