9 Out Of 24 As A Percentage
Treneri
May 10, 2025 · 5 min read
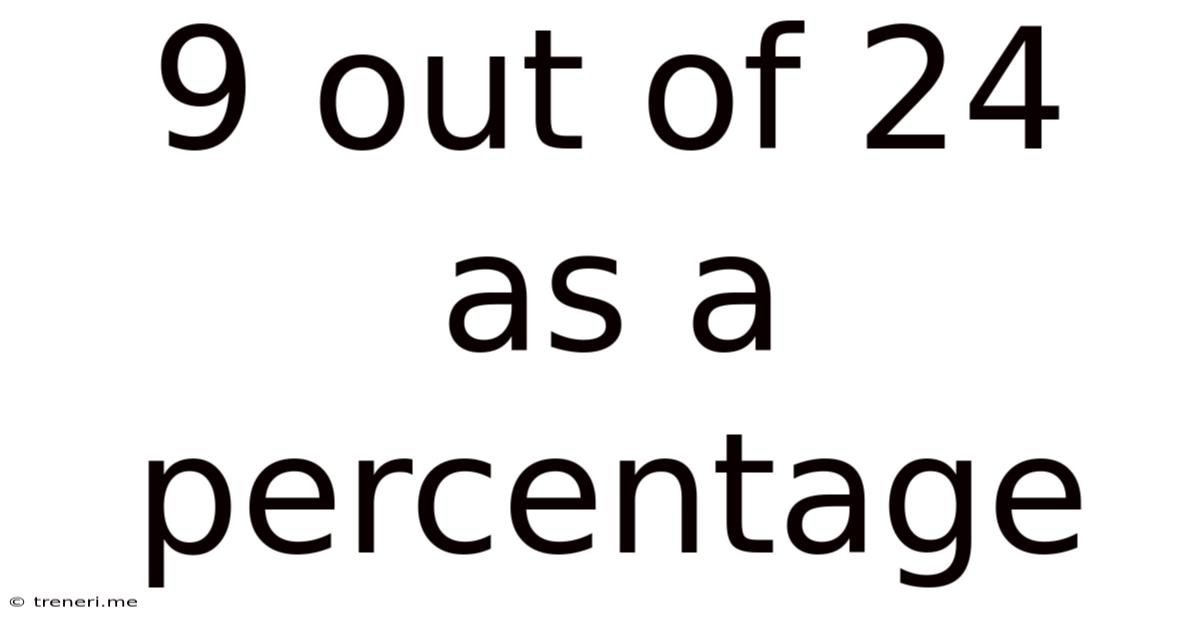
Table of Contents
9 out of 24 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This comprehensive guide delves into the specifics of calculating "9 out of 24 as a percentage," exploring different methods, offering practical examples, and providing a deeper understanding of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Percentages are used to represent proportions, often to express a part of a whole. For example, scoring 80% on a test means you answered 80 out of 100 questions correctly.
Converting Fractions to Percentages: The Basic Formula
The fundamental formula for converting a fraction to a percentage is:
(Part / Whole) * 100%
In our case, "9 out of 24" represents the fraction 9/24. Applying the formula:
(9 / 24) * 100% = 37.5%
Therefore, 9 out of 24 is 37.5%.
Step-by-Step Calculation: 9 out of 24
Let's break down the calculation step-by-step for clarity:
-
Identify the parts: We have 9 (the part) and 24 (the whole).
-
Form the fraction: Represent the relationship as a fraction: 9/24.
-
Simplify the fraction (optional but recommended): Both 9 and 24 are divisible by 3. Simplifying the fraction gives us 3/8. This makes the subsequent calculation easier.
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
-
Multiply by 100: Multiply the decimal by 100 to express it as a percentage: 0.375 * 100 = 37.5
-
Add the percentage symbol: The final answer is 37.5%.
Alternative Methods for Calculating Percentages
While the basic formula is universally applicable, alternative methods can be used depending on the complexity of the fraction and the tools available.
Using a Calculator
Most calculators have a percentage function. Simply enter 9 ÷ 24 and then press the "%" button. The calculator will automatically perform the multiplication by 100 and display the result as 37.5%.
Using Spreadsheet Software (e.g., Microsoft Excel or Google Sheets)
Spreadsheets offer powerful tools for percentage calculations. You can enter the fraction (9/24) directly into a cell, and the software will automatically display it as a decimal. Formatting the cell to display as a percentage will give you the 37.5% result. Alternatively, you can use the formula =(9/24)*100 in a cell.
Mental Math Techniques (for simpler fractions)
For simpler fractions, mental math can be quicker. Recognizing that 1/8 is 12.5% (because 1/8 * 100 = 12.5), you can easily calculate 3/8 as 3 * 12.5% = 37.5%. This approach requires practice and familiarity with common fraction-percentage equivalents.
Practical Applications of Percentage Calculations: Real-World Examples
Understanding how to calculate percentages is vital in many real-world scenarios. Here are some examples demonstrating the practical applications of this skill:
1. Sales and Discounts
A store offers a 25% discount on an item originally priced at $100. To calculate the discount amount:
25% of $100 = (25/100) * $100 = $25
The discounted price would be $100 - $25 = $75. Understanding percentage discounts helps consumers make informed purchase decisions.
2. Grade Calculation
A student answers 18 out of 25 questions correctly on a test. To calculate the percentage score:
(18/25) * 100% = 72%
The student scored 72% on the test. This demonstrates the application of percentages in academic assessments.
3. Financial Calculations
A person invests $5000 and earns $250 in interest. To calculate the return on investment (ROI) as a percentage:
($250/$5000) * 100% = 5%
The ROI is 5%. This highlights the use of percentages in evaluating financial performance.
4. Statistics and Data Analysis
In a survey of 200 people, 90 prefer Brand A. To determine the percentage of people who prefer Brand A:
(90/200) * 100% = 45%
45% of respondents prefer Brand A. This shows the relevance of percentages in interpreting survey data.
5. Budgeting and Expense Tracking
A person budgets $2000 per month and spends $500 on rent. To find the percentage of their budget spent on rent:
($500/$2000) * 100% = 25%
25% of their monthly budget is allocated to rent. This example illustrates the use of percentages in personal finance management.
Beyond the Basics: Advanced Percentage Concepts
While calculating "9 out of 24 as a percentage" serves as a foundational example, understanding more advanced percentage concepts will enhance your numerical skills. These include:
-
Percentage increase and decrease: Calculating the percentage change between two values. For instance, finding the percentage increase in sales from one year to the next.
-
Compound interest: Calculating interest earned not only on the principal amount but also on accumulated interest. This is a core concept in financial planning.
-
Percentage points: Understanding the difference between a percentage change and percentage points. For example, a change from 20% to 25% is a 5 percentage point increase, but a 25% increase in the initial value.
-
Working with percentages in complex scenarios: Applying percentages to multiple variables or within more intricate equations.
Mastering these advanced concepts will broaden your understanding of percentages and their applications in various fields.
Conclusion: Mastering Percentage Calculations
The ability to convert fractions to percentages is a valuable skill applicable in numerous contexts. Understanding the fundamental formula, exploring alternative calculation methods, and practicing with real-world examples will solidify your understanding. This guide provides a comprehensive resource for calculating percentages, enabling you to confidently tackle various numerical challenges. As you progress, delve into more advanced percentage concepts to deepen your understanding and enhance your problem-solving abilities. Remember, consistent practice and application are key to mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
What Is 90 Days From July 12 2024
May 10, 2025
-
90 Days After May 19 2024
May 10, 2025
-
What Is 27 30 As A Grade
May 10, 2025
-
What Is The Greatest Common Factor Of 48 And 42
May 10, 2025
-
56 Grams Is Equal To How Many Ounces
May 10, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 24 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.