9 Out Of 27 As A Percentage
Treneri
May 13, 2025 · 4 min read
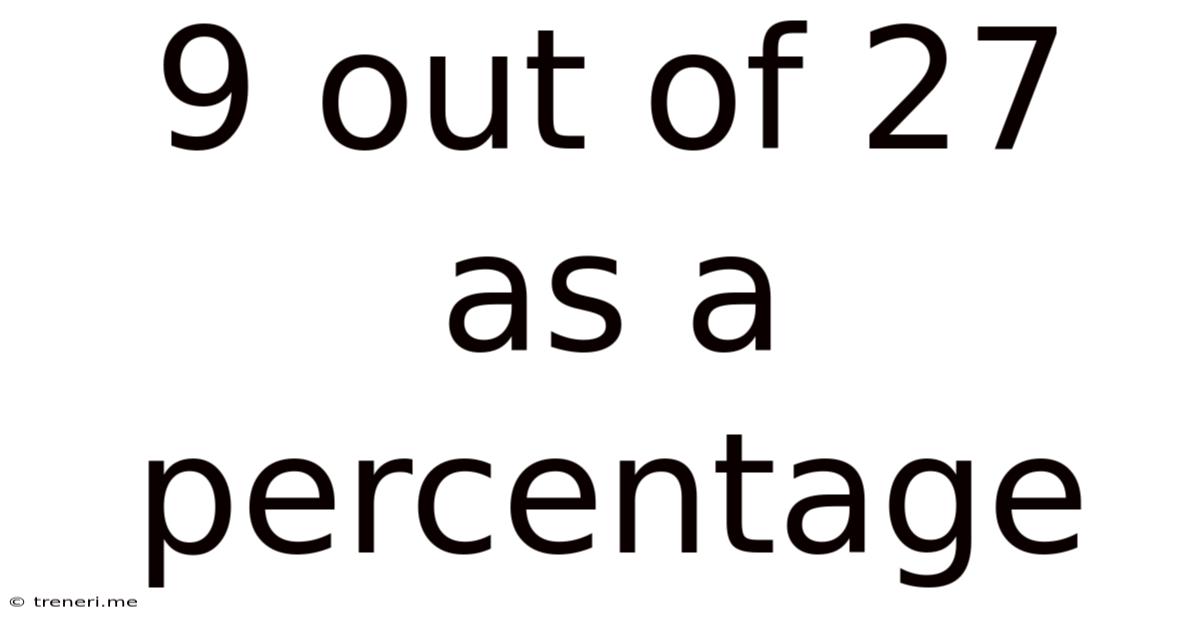
Table of Contents
9 Out of 27 as a Percentage: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This comprehensive guide will delve into the calculation of "9 out of 27 as a percentage," explaining the process step-by-step and providing valuable context for broader percentage calculations. We'll also explore practical applications and tackle common misconceptions.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage represents a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% signifies 50 out of 100, or 50/100, which simplifies to 1/2.
Understanding this fundamental relationship allows us to convert between fractions, decimals, and percentages effortlessly. This conversion is key to accurately calculating percentages in various scenarios.
Calculating 9 Out of 27 as a Percentage: The Step-by-Step Approach
To determine what percentage 9 represents of 27, we follow these straightforward steps:
Step 1: Formulate the Fraction:
The first step involves expressing the problem as a fraction. "9 out of 27" translates directly to the fraction 9/27.
Step 2: Simplify the Fraction (Optional but Recommended):
Simplifying the fraction makes the subsequent calculation easier. Both the numerator (9) and the denominator (27) are divisible by 9. Dividing both by 9, we get the simplified fraction 1/3.
Step 3: Convert the Fraction to a Decimal:
To convert the fraction 1/3 to a decimal, we perform the division: 1 ÷ 3 = 0.3333... (the 3s repeat infinitely).
Step 4: Convert the Decimal to a Percentage:
Finally, we convert the decimal to a percentage by multiplying by 100: 0.3333... × 100 = 33.33...%
Therefore, 9 out of 27 is 33.33% (approximately). The recurring decimal indicates that the percentage is a repeating decimal, and it's often rounded to a certain number of decimal places depending on the context. For most practical purposes, rounding to two decimal places (33.33%) is sufficient.
Alternative Calculation Method: Direct Percentage Calculation
Instead of simplifying the fraction first, we can directly calculate the percentage using the following formula:
(Part / Whole) * 100% = Percentage
In this case:
(9 / 27) * 100% = 0.3333... * 100% = 33.33...%
This method achieves the same result, demonstrating the flexibility in approaching percentage calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages has a wide array of practical applications in various fields:
1. Finance and Budgeting:
- Interest Rates: Calculating interest earned on savings accounts or interest paid on loans involves percentages.
- Discounts and Sales Tax: Determining the final price of an item after a discount or adding sales tax requires percentage calculations.
- Investment Returns: Analyzing investment performance often involves assessing returns as percentages.
2. Statistics and Data Analysis:
- Proportions and Ratios: Percentages are crucial for expressing proportions within datasets. For example, calculating the percentage of respondents who prefer a particular product in a survey.
- Data Representation: Charts and graphs often utilize percentages to visually represent data distributions and proportions.
3. Everyday Life:
- Tipping: Calculating tips in restaurants often involves calculating a percentage of the bill.
- Grade Calculation: Many educational systems use percentages to represent student grades.
- Ingredient Ratios: In cooking and baking, recipes often list ingredients as percentages of the total weight or volume.
Common Mistakes to Avoid in Percentage Calculations
While percentage calculations are relatively straightforward, common errors can occur:
- Incorrect Fraction Setup: Ensure the correct part and whole are used when forming the initial fraction.
- Rounding Errors: Be mindful of rounding errors, especially when dealing with repeating decimals. The level of precision required depends on the context.
- Misunderstanding the Percentage Meaning: Remember that a percentage is always relative to the whole.
- Using the Incorrect Formula: Using the wrong formula will yield an inaccurate result. Ensure you utilize the appropriate formula for the specific situation.
Advanced Percentage Calculations: Beyond the Basics
While the 9 out of 27 example provides a basic framework, many real-world applications involve more complex scenarios. These might include:
- Calculating Percentage Change: This involves determining the percentage increase or decrease between two values. The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100%.
- Compounding Percentages: This is crucial in finance, where interest or growth is calculated on the accumulated amount.
- Percentage Points vs. Percentages: It's important to distinguish between percentage points and percentages. A change from 10% to 15% is a 5 percentage point increase, but a 50% increase in the original percentage.
Conclusion: Mastering Percentage Calculations for Success
Understanding and mastering percentage calculations is a vital skill for success in numerous areas of life, from personal finance to professional endeavors. By understanding the fundamental principles, employing the correct formula, and avoiding common errors, you can confidently tackle any percentage calculation problem. The ability to interpret and utilize percentages effectively contributes to informed decision-making and a deeper understanding of quantitative information. Remember to always double-check your work and consider the level of precision required based on the context of the problem. This thorough understanding of percentage calculation will empower you to navigate various numerical challenges and succeed in diverse situations.
Latest Posts
Latest Posts
-
How Much Is 200 Grams In Lbs
May 13, 2025
-
Cuanto Es 2 Onzas En Cucharadas
May 13, 2025
-
Which Solid Has A Greater Volume 8 3 6 2
May 13, 2025
-
How To Find Y Intercept With A Point And Slope
May 13, 2025
-
What Size Ring Is 2 1 2 Inches
May 13, 2025
Related Post
Thank you for visiting our website which covers about 9 Out Of 27 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.