90 Divided By 18 With Remainder
Treneri
May 10, 2025 · 4 min read
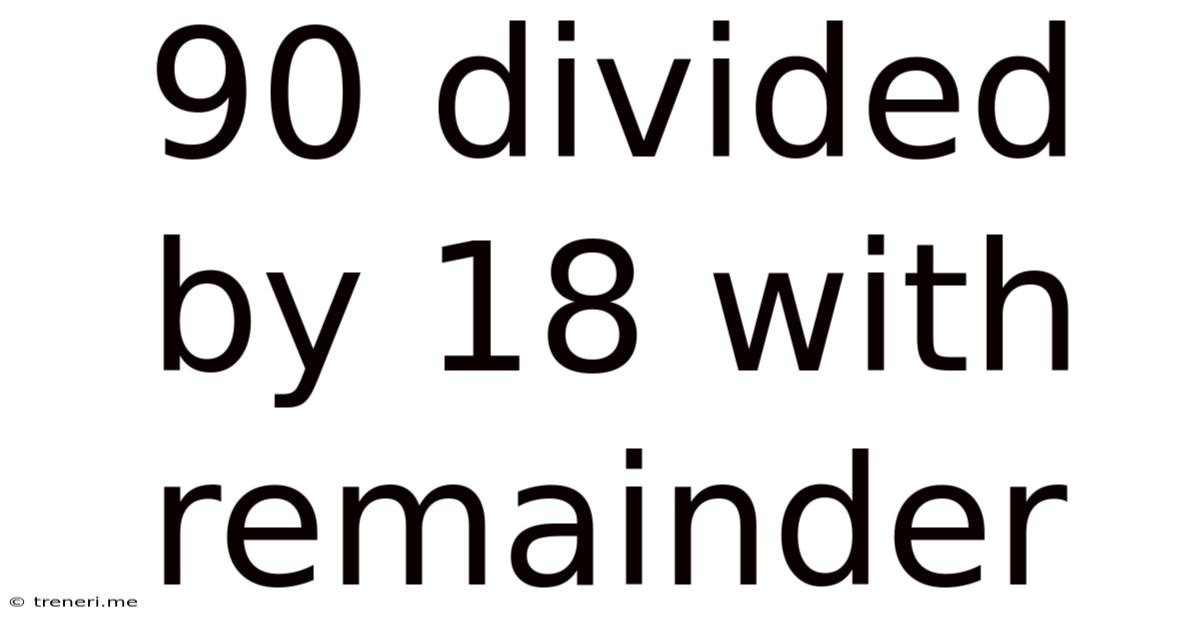
Table of Contents
90 Divided by 18 with Remainder: A Deep Dive into Division
This article explores the seemingly simple mathematical problem of dividing 90 by 18, focusing on understanding not just the quotient but also the remainder. While the answer might seem instantly obvious to some, we'll delve into the underlying concepts, explore different methods of solving the problem, and discuss the broader applications of division with remainders in various fields. This in-depth analysis will be valuable for students learning division, educators looking for engaging teaching methods, and anyone curious about the fascinating world of mathematics.
Understanding Division and Remainders
Division is a fundamental arithmetic operation that involves splitting a quantity into equal parts. When we divide 90 by 18, we're asking: "How many times does 18 fit into 90?" The result of this operation is composed of two key parts: the quotient and the remainder.
- Quotient: The quotient represents the number of times the divisor (18) goes into the dividend (90) completely.
- Remainder: The remainder is the amount left over after dividing as many times as possible without going over.
In the context of 90 divided by 18, we're aiming to find both the quotient and the remainder.
Methods for Solving 90 ÷ 18
Several methods can be employed to solve this division problem, each offering a unique perspective and strengthening understanding.
1. Long Division
Long division is a systematic approach that's widely taught in schools. It involves a step-by-step process of dividing, multiplying, subtracting, and bringing down digits.
5
18 | 90
-90
--
0
This method clearly shows that 18 goes into 90 exactly 5 times, with no remainder. Therefore, the quotient is 5, and the remainder is 0.
2. Repeated Subtraction
Repeated subtraction provides a more intuitive, visual approach to division. We repeatedly subtract the divisor (18) from the dividend (90) until we reach a number smaller than the divisor. The number of times we subtract is the quotient, and the remaining number is the remainder.
90 - 18 = 72 72 - 18 = 54 54 - 18 = 36 36 - 18 = 18 18 - 18 = 0
We subtracted 18 five times before reaching 0, so the quotient is 5, and the remainder is 0.
3. Multiplication Tables
Familiarity with multiplication tables provides a quick way to solve this problem. We can ask: "What number multiplied by 18 equals 90?" Knowing our 18 times table (or using a calculator to verify), we find that 18 x 5 = 90. This immediately reveals a quotient of 5 and a remainder of 0.
The Significance of Remainders
While the example of 90 divided by 18 results in a remainder of 0 (meaning 18 divides 90 evenly), remainders are crucial in many other division problems. Understanding remainders allows us to:
-
Solve real-world problems: Imagine distributing 92 cookies equally among 18 children. Dividing 92 by 18 gives a quotient of 5 (each child gets 5 cookies) and a remainder of 2 (there are 2 cookies left over).
-
Represent fractional parts: A remainder can be expressed as a fraction. If we divided 92 by 18, the remainder of 2 can be represented as 2/18, which simplifies to 1/9. This means each child gets 5 and 1/9 cookies.
-
Work with modular arithmetic: Remainders are fundamental in modular arithmetic (also known as clock arithmetic), which has applications in cryptography, computer science, and other fields.
Applications of Division with Remainders
The concept of division with remainders finds applications across various disciplines:
1. Everyday Life
- Sharing items: Distributing items equally among a group of people often leaves a remainder.
- Measurement: Converting units of measurement (e.g., converting inches to feet) sometimes involves remainders.
- Time: Calculating the number of weeks in a given number of days will often yield a remainder representing the extra days.
2. Computer Science
- Data structures: Hashing algorithms and other data structures use modular arithmetic (based on remainders) to manage data efficiently.
- Cryptography: Cryptographic techniques often rely on modular arithmetic for secure communication.
- Error detection: Checksums and other error-detection codes utilize remainders to detect data corruption.
3. Engineering
- Material allocation: Cutting materials to specific sizes might leave remainders of unusable material.
- Resource management: Allocating resources (time, budget, etc.) across different projects often results in remainders.
4. Mathematics
- Number theory: Remainders play a crucial role in number theory, the study of integers and their properties.
- Abstract algebra: Concepts related to remainders are essential in abstract algebra, a more advanced area of mathematics.
Expanding the Understanding
While this article focused on 90 divided by 18, the principles discussed are applicable to any division problem. Practicing various division problems with remainders, exploring different solution methods, and understanding the applications of remainders in diverse fields will strengthen your mathematical abilities.
Conclusion: Mastering Division with Remainders
The seemingly straightforward calculation of 90 divided by 18 provides a springboard for a deeper understanding of division, remainders, and their far-reaching implications. By exploring various solution methods and recognizing the real-world applications of remainders, we move beyond simply finding an answer to grasping the core mathematical concepts and their relevance in a variety of contexts. This thorough exploration equips learners and enthusiasts alike with a more robust understanding of this fundamental arithmetic operation. The power of understanding remainders extends well beyond basic calculations, permeating various fields and fostering critical thinking skills applicable across numerous disciplines.
Latest Posts
Latest Posts
-
What Grade Is A 33 Out Of 40
May 10, 2025
-
What Is A 2 Slope In Inches
May 10, 2025
-
How Do You Calculate A Perimeter
May 10, 2025
-
How Much Is 250 Km In Miles
May 10, 2025
-
4 5 Minus 1 2 In Fraction Form
May 10, 2025
Related Post
Thank you for visiting our website which covers about 90 Divided By 18 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.