90 To 130 Is What Percentage Increase
Treneri
May 13, 2025 · 5 min read
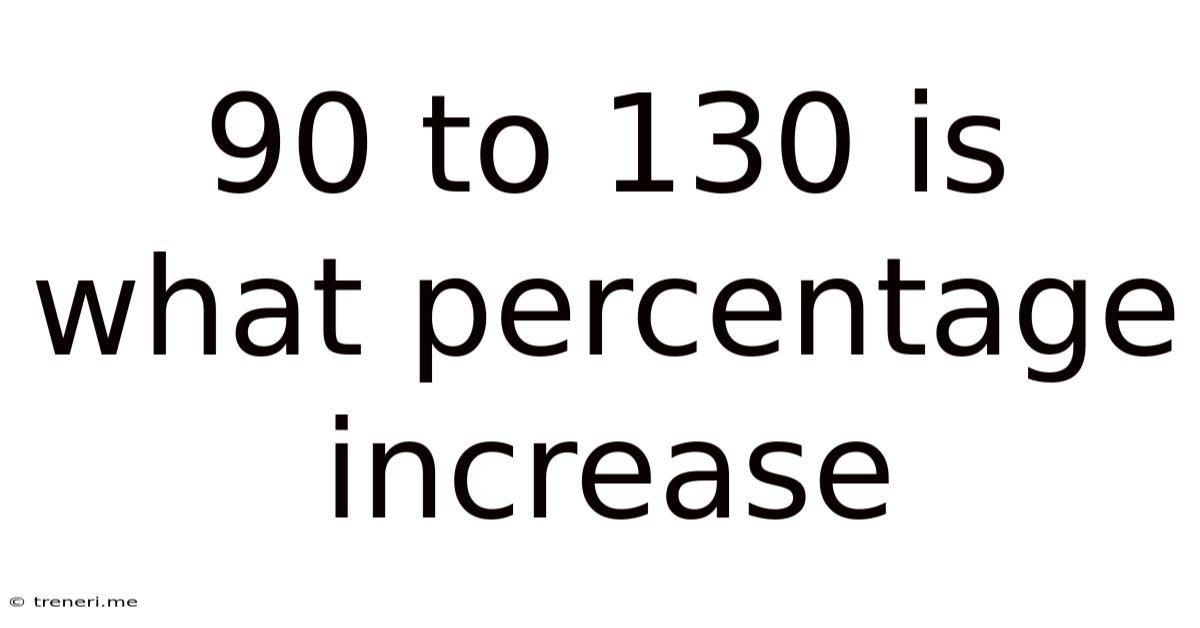
Table of Contents
90 to 130 is What Percentage Increase? A Comprehensive Guide
Calculating percentage increases is a fundamental skill with broad applications across various fields, from finance and business to everyday life. Understanding how to perform these calculations accurately is crucial for making informed decisions and interpreting data effectively. This article will delve deep into the calculation of the percentage increase from 90 to 130, providing a step-by-step guide, exploring common mistakes, and showcasing practical applications.
Understanding Percentage Increase
Before tackling the specific calculation, let's clarify the concept of percentage increase. A percentage increase represents the relative change between an initial value and a final value, expressed as a percentage of the initial value. The formula is straightforward:
Percentage Increase = [(Final Value - Initial Value) / Initial Value] × 100%
This formula tells us how much the value has grown relative to its starting point. The result is always a positive number if the final value is greater than the initial value, indicating an increase. If the final value is smaller than the initial value, the result will be negative, indicating a percentage decrease.
Calculating the Percentage Increase from 90 to 130
Now, let's apply this formula to our specific problem: determining the percentage increase from 90 to 130.
-
Identify the Initial Value and Final Value:
- Initial Value = 90
- Final Value = 130
-
Substitute the Values into the Formula:
Percentage Increase = [(130 - 90) / 90] × 100%
-
Perform the Calculation:
- (130 - 90) = 40
- 40 / 90 = 0.4444...
- 0.4444... × 100% ≈ 44.44%
Therefore, the percentage increase from 90 to 130 is approximately 44.44%.
Common Mistakes to Avoid
While the calculation itself is relatively simple, several common errors can lead to inaccurate results. Let's examine some of these:
-
Reversing the Initial and Final Values: Ensure you correctly identify the initial and final values. Subtracting the initial value from the final value is crucial. Reversing them will yield a negative result, incorrectly indicating a decrease.
-
Incorrect Order of Operations: Follow the order of operations (PEMDAS/BODMAS): Parentheses/Brackets first, then Exponents/Orders, then Multiplication and Division (from left to right), and finally Addition and Subtraction (from left to right).
-
Rounding Errors: Be mindful of rounding during the calculation. Rounding too early can significantly impact the final result. It's best to keep as many decimal places as possible until the final answer, then round appropriately based on the context (e.g., to two decimal places for percentage calculations).
-
Using the Wrong Formula: Ensure you're using the correct percentage increase formula. Confusing it with other percentage calculations, such as percentage difference or percentage change, can lead to incorrect results.
Practical Applications of Percentage Increase Calculations
Understanding percentage increase calculations is invaluable in numerous real-world scenarios:
-
Finance: Tracking investment returns, calculating interest earned, analyzing profit margins, and evaluating the growth of savings accounts all rely on percentage increase calculations. For example, a 44.44% increase in investment value represents a substantial gain.
-
Business: Analyzing sales growth, comparing market share, measuring productivity improvements, and assessing the effectiveness of marketing campaigns all involve percentage increase calculations. A 44.44% increase in sales is a strong indicator of business success.
-
Economics: Tracking inflation rates, measuring economic growth (GDP), analyzing changes in employment figures, and evaluating changes in consumer spending all rely on percentage increase calculations. Understanding these changes is vital for economists and policymakers.
-
Science: Scientists frequently use percentage increases to quantify experimental results, track population growth in ecological studies, and analyze data from various scientific experiments.
-
Everyday Life: Calculating discounts, understanding tax increases, comparing prices, and tracking personal savings all benefit from understanding percentage increases.
Beyond the Basics: Advanced Considerations
While the basic formula provides a straightforward approach, more complex situations may require additional considerations:
-
Compounding: In scenarios where the percentage increase is applied repeatedly over time (e.g., compound interest), the calculation becomes more intricate. Compounding significantly magnifies the overall growth over time.
-
Multiple Percentage Increases: If multiple percentage increases are applied sequentially, it's crucial to apply each increase to the previous result, not the original value. Simply adding the percentages will yield an inaccurate result.
-
Percentage Decrease: Remember that the formula can also be used to calculate percentage decreases, resulting in a negative value.
Example Scenarios using 44.44% Increase
Let's illustrate the practical application of a 44.44% increase with a few examples:
Scenario 1: Investment Growth
If you invested $90 and saw a 44.44% increase, your investment would now be worth:
$90 + ($90 * 0.4444) = $129.99 (approximately $130)
Scenario 2: Sales Increase
If a company sold 90 units last year and experienced a 44.44% increase this year, they sold:
90 + (90 * 0.4444) = 129.99 (approximately 130) units this year.
Scenario 3: Salary Increase
If someone earned $90 per hour and received a 44.44% raise, their new hourly wage would be:
$90 + ($90 * 0.4444) = $129.99 (approximately $130) per hour.
Conclusion
Calculating percentage increases is a fundamental skill with widespread applications. Understanding the formula, avoiding common mistakes, and appreciating the practical applications are crucial for effective data interpretation and informed decision-making in various aspects of life. While the calculation from 90 to 130 provides a straightforward example, remember to adapt your approach for more complex scenarios, such as compounding and multiple percentage changes. Mastering this skill empowers you to analyze data, make informed decisions, and navigate the numerical world with greater confidence. Remember to always double-check your calculations and consider the context of the problem to ensure accurate and meaningful results.
Latest Posts
Latest Posts
-
Exponential Function That Passes Through Points
May 13, 2025
-
How Many Leaves On A Maple Tree
May 13, 2025
-
Cuanto Es 1 4 De Acre En Pies
May 13, 2025
-
Calculate The Area Of The Following Figure
May 13, 2025
-
Cuantos Bloques En El Nether Son En El Overworld
May 13, 2025
Related Post
Thank you for visiting our website which covers about 90 To 130 Is What Percentage Increase . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.