948 Divided By 10 To The 3rd Power
Treneri
May 07, 2025 · 4 min read
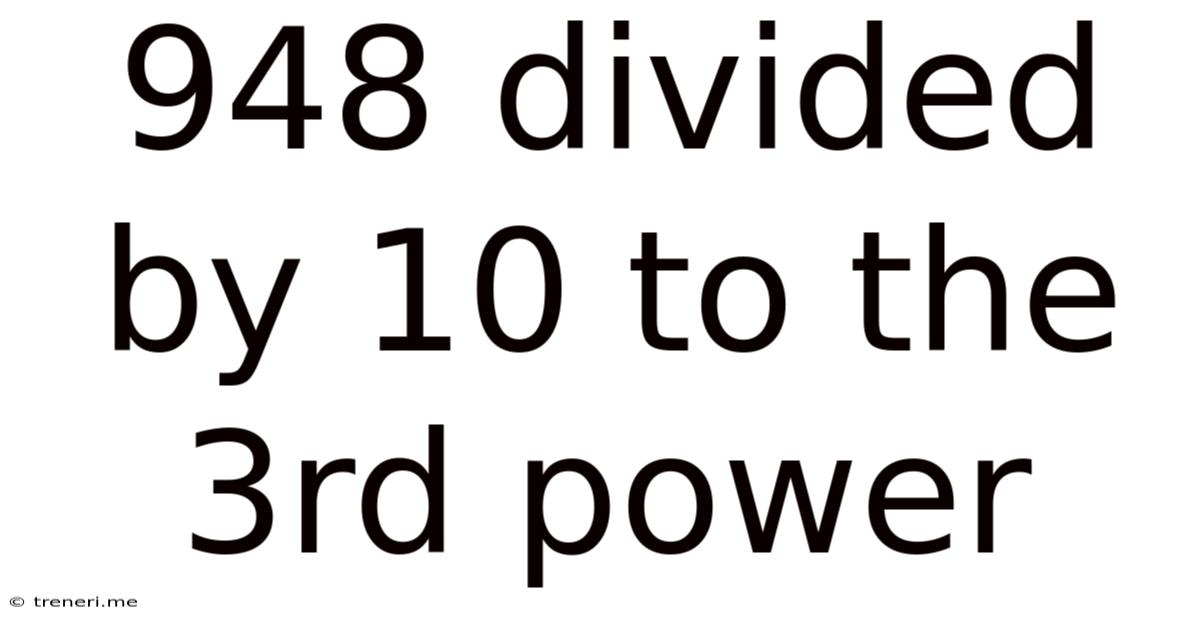
Table of Contents
948 Divided by 10 to the 3rd Power: A Deep Dive into Decimal Shifting
This article explores the seemingly simple mathematical operation of dividing 948 by 10 to the 3rd power (10³), unpacking the underlying principles, exploring various methods of calculation, and highlighting the broader implications within the context of scientific notation and decimal manipulation. We'll delve beyond the basic answer to understand the fundamental concepts involved and how this type of calculation is used in diverse fields.
Understanding the Problem: 948 ÷ 10³
The core problem is to calculate 948 divided by 1000 (since 10³ = 10 x 10 x 10 = 1000). This is a common type of calculation encountered in various scientific, engineering, and financial contexts. Understanding how to solve it efficiently and accurately is crucial.
The Significance of Powers of 10
Powers of 10 (10¹, 10², 10³, 10⁴, etc.) represent a fundamental concept in mathematics, particularly in working with large and small numbers. They provide a concise way to express numbers using exponents, significantly simplifying calculations and improving readability. Understanding powers of 10 is critical for handling scientific notation and performing calculations involving unit conversions.
Methods for Calculating 948 ÷ 10³
Several approaches can be used to calculate 948 ÷ 10³. We will examine three common methods:
1. Direct Division:
This involves the straightforward process of long division: dividing 948 by 1000.
0.948
1000 | 948.000
9000
----
480
400
---
800
800
---
0
This method yields the answer 0.948.
2. Decimal Point Shifting:
This method leverages the properties of powers of 10. Dividing by 10³ (1000) is equivalent to moving the decimal point three places to the left.
Since 948 can be written as 948.000, moving the decimal point three places to the left gives us 0.948. This method is significantly faster and more efficient than long division for calculations involving powers of 10.
3. Scientific Notation:
Expressing numbers in scientific notation provides a powerful approach to handling very large or very small numbers. 948 can be written in scientific notation as 9.48 x 10².
Dividing this by 10³ involves subtracting the exponents:
(9.48 x 10²) ÷ 10³ = 9.48 x 10²⁻³ = 9.48 x 10⁻¹ = 0.948
This method showcases the elegance and efficiency of scientific notation, particularly useful for complex calculations involving multiple powers of 10.
Practical Applications and Real-World Examples
The seemingly simple calculation of 948 ÷ 10³ has a wide array of applications in various fields:
1. Unit Conversions:
Imagine converting cubic meters to cubic millimeters. There are 1000 millimeters in a meter, so 1 cubic meter equals 10³ cubic millimeters. If you have 948 cubic meters, you would use this division to find the equivalent volume in cubic millimeters: 948 cubic meters * 1000 mm³/m³ = 948000 cubic millimeters. Conversely, to convert cubic millimeters to cubic meters, you'd divide by 1000.
2. Financial Calculations:
In finance, dealing with percentages often involves calculations similar to this. For example, if a company's profit is 948,000 dollars and you need to calculate 0.1% of the profit (one-thousandth of the profit), you would effectively be performing 948,000 ÷ 1000 = 948 dollars.
3. Scientific Measurements:
In scientific measurements, extremely small quantities are frequently expressed using powers of 10. For example, converting nanometers (10⁻⁹ meters) to meters or converting milligrams (10⁻³ grams) to grams requires calculations that involve dividing or multiplying by powers of 10, similar to the example we’ve been working with.
Expanding the Concept: Generalizing Division by Powers of 10
The principles explored with 948 ÷ 10³ are readily generalizable to dividing any number by any positive power of 10. The key is to understand that dividing by 10ⁿ is equivalent to shifting the decimal point n places to the left.
For instance:
- 4567 ÷ 10² = 45.67 (Decimal point shifted two places to the left)
- 12.345 ÷ 10¹ = 1.2345 (Decimal point shifted one place to the left)
- 0.0089 ÷ 10⁻² = 0.89 (Dividing by 10⁻² is the same as multiplying by 10², shifting the decimal two places to the right)
Understanding this generalization is crucial for efficient computation and developing numerical fluency.
Conclusion: Mastering Decimal Manipulation
This detailed exploration of 948 divided by 10 to the 3rd power reveals more than just a simple arithmetic solution. It underscores the importance of understanding powers of 10, the efficiency of decimal point shifting, and the elegance of scientific notation. The ability to perform these calculations swiftly and accurately is an essential skill across various scientific, engineering, financial, and everyday contexts. Mastering this fundamental concept forms a solid foundation for tackling more complex mathematical problems involving decimal manipulation and numerical analysis. The practical applications extend far beyond the immediate calculation, highlighting the pervasive nature of powers of 10 in quantifying the world around us.
Latest Posts
Latest Posts
-
How High Does Uv Index Have To Be To Tan
May 08, 2025
-
Cuanto Es 10 Onzas En Libras
May 08, 2025
-
How Many Days Are In 21 Years
May 08, 2025
-
What Is The Slope Of A Triangle
May 08, 2025
-
What Is 10 Percent Of 10000 Dollars
May 08, 2025
Related Post
Thank you for visiting our website which covers about 948 Divided By 10 To The 3rd Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.