95 Of 40 Is What Number
Treneri
May 11, 2025 · 4 min read
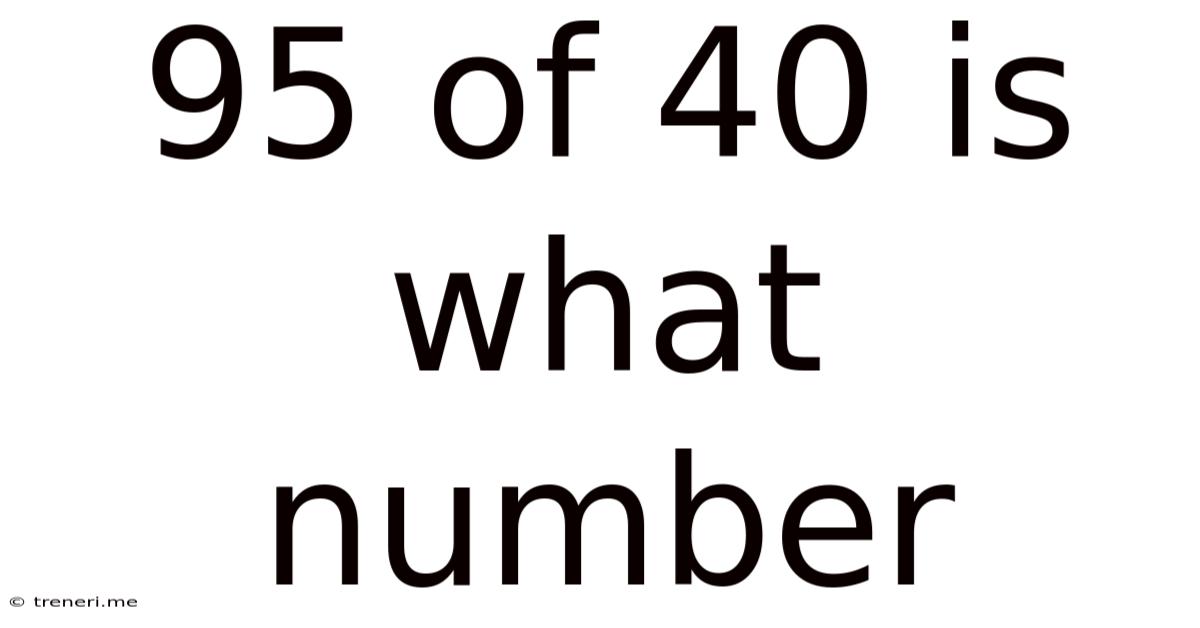
Table of Contents
95% of 40 is What Number? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. Understanding how to determine a percentage of a number is crucial for making informed decisions and accurately interpreting data. This comprehensive guide will delve into the calculation of 95% of 40, providing multiple methods, explanations, and real-world examples. We'll also explore the broader concept of percentages and how to solve similar percentage problems.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25.
Percentages are a convenient way to represent parts of a whole, making comparisons and interpretations easier. They are used extensively in various contexts, including:
- Finance: Interest rates, discounts, taxes, profit margins
- Statistics: Data representation, probability calculations
- Science: Concentration measurements, experimental results
- Everyday life: Sales, tips, discounts
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method for calculating 95% of 40.
Step 1: Convert the percentage to a decimal.
To convert a percentage to a decimal, divide the percentage by 100. In this case:
95% / 100 = 0.95
Step 2: Multiply the decimal by the number.
Now, multiply the decimal equivalent (0.95) by the number you want to find the percentage of (40):
0.95 * 40 = 38
Therefore, 95% of 40 is 38.
Method 2: Using Fractions
This method utilizes the fractional representation of percentages.
Step 1: Express the percentage as a fraction.
95% can be expressed as the fraction 95/100.
Step 2: Simplify the fraction (optional).
The fraction 95/100 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 5:
95/100 = 19/20
Step 3: Multiply the fraction by the number.
Multiply the simplified fraction (19/20) by 40:
(19/20) * 40 = 19 * (40/20) = 19 * 2 = 38
Therefore, 95% of 40 is 38. This method demonstrates the underlying fractional nature of percentages.
Method 3: Proportion Method
The proportion method offers a more visual approach to solving percentage problems. It's particularly useful for understanding the relationship between the parts and the whole.
Step 1: Set up a proportion.
We can set up a proportion to represent the problem:
95/100 = x/40
Where 'x' represents the unknown value (95% of 40).
Step 2: Cross-multiply.
Cross-multiply the terms in the proportion:
95 * 40 = 100 * x
Step 3: Solve for x.
3800 = 100x
x = 3800 / 100
x = 38
Therefore, 95% of 40 is 38. This method highlights the proportional relationship between the percentage and the resulting value.
Real-World Applications of Percentage Calculations
Understanding percentage calculations has numerous practical applications. Let's explore a few:
Sales and Discounts
Imagine a store offering a 95% discount on a $40 item. Using the methods described above, we can quickly calculate the discount amount: 95% of $40 = $38. This means the discounted price would be $40 - $38 = $2.
Tax Calculations
Calculating sales tax is another common application. If the sales tax rate is 9.5%, and you purchase an item for $40, the tax amount would be 9.5% of $40 = $3.80. Your total cost would be $40 + $3.80 = $43.80.
Financial Analysis
Percentage calculations are essential in financial analysis, such as calculating profit margins, interest earned, and return on investment (ROI). Understanding these percentages helps in making informed financial decisions.
Statistical Analysis
Percentages play a crucial role in statistical analysis, allowing for easy comparison and interpretation of data sets. For example, expressing survey results as percentages simplifies the understanding of proportions within a population.
Scientific Applications
In scientific fields, percentages are used to represent concentrations, yields in experiments, and error rates. Accurate percentage calculations are vital for reliable scientific research.
Solving Similar Percentage Problems
The techniques used to calculate 95% of 40 are readily applicable to solving other percentage problems. Simply replace the percentage and the number with the values relevant to your specific problem. Remember the three methods: converting to decimals, using fractions, and using proportions.
For example:
- What is 60% of 80? Using the decimal method: 0.60 * 80 = 48
- What is 25% of 120? Using the fraction method: (25/100) * 120 = 30
- What is 15% of 500? Using the proportion method: 15/100 = x/500; x = 75
Conclusion
Calculating 95% of 40, resulting in 38, is a straightforward yet important skill. Understanding the different methods—decimal conversion, fraction method, and proportion method—enhances your ability to tackle various percentage calculations in diverse real-world situations. Mastering percentage calculations empowers you to analyze data effectively, make informed decisions, and navigate various numerical challenges confidently. Remember to practice regularly and apply these methods to different scenarios to solidify your understanding and build your confidence.
Latest Posts
Latest Posts
-
How To Calculate Home Equity Line Of Credit Monthly Payment
May 12, 2025
-
What Uv Can U Tan In
May 12, 2025
-
What Is The Area Of The Pentagon Shown Below
May 12, 2025
-
What Is A 17 Out Of 20 Grade
May 12, 2025
-
How Many Kg Is 17 Lbs
May 12, 2025
Related Post
Thank you for visiting our website which covers about 95 Of 40 Is What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.