95 Out Of 120 As A Percentage
Treneri
May 12, 2025 · 4 min read
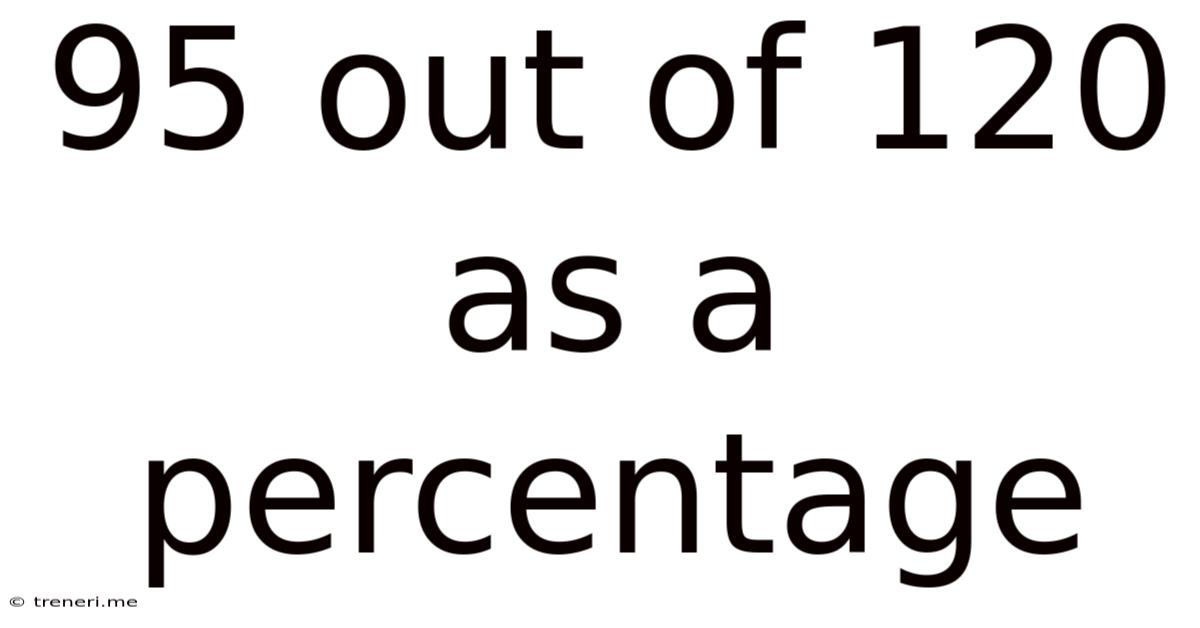
Table of Contents
95 out of 120 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This comprehensive guide will delve into calculating "95 out of 120 as a percentage," providing a detailed explanation of the process and exploring various related concepts and applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are a convenient way to standardize proportions, making it easy to compare different quantities and visualize ratios.
Calculating 95 out of 120 as a Percentage
To calculate 95 out of 120 as a percentage, we follow these steps:
-
Formulate the Fraction: Express the given numbers as a fraction. In this case, it's 95/120. This represents 95 parts out of a total of 120 parts.
-
Convert the Fraction to a Decimal: Divide the numerator (95) by the denominator (120): 95 ÷ 120 = 0.791666...
-
Convert the Decimal to a Percentage: Multiply the decimal by 100: 0.791666... × 100 = 79.1666...%
-
Round the Percentage: Depending on the desired level of precision, round the percentage to a suitable number of decimal places. Rounding to two decimal places gives us 79.17%.
Therefore, 95 out of 120 is 79.17%.
Alternative Calculation Method: Using Proportions
Another way to approach this calculation involves setting up a proportion:
Let x be the percentage we want to find.
We can set up the proportion:
95/120 = x/100
To solve for x, cross-multiply:
95 * 100 = 120 * x
9500 = 120x
x = 9500/120
x = 79.1666...
Again, rounding to two decimal places yields 79.17%.
Practical Applications of Percentage Calculations
The ability to calculate percentages has widespread applications in various aspects of life:
1. Academic Performance:
-
Grade Calculation: Many grading systems use percentages to represent a student's performance on tests and assignments. Understanding percentage calculations allows students to accurately assess their progress and identify areas for improvement. For example, scoring 95 out of 120 on an exam reflects strong performance.
-
Overall Grade Point Average (GPA): GPAs are often calculated using a weighted average of grades, where each grade is expressed as a percentage.
2. Financial Management:
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating percentages is crucial for understanding the cost of borrowing or the return on investment.
-
Discounts and Sales Tax: Sales often involve percentage discounts, while sales tax is typically added as a percentage of the purchase price. Calculating these percentages ensures accurate pricing.
-
Budgeting: Tracking expenses and allocating funds often requires calculating percentages of a total budget. This allows for effective financial planning and monitoring.
3. Data Analysis and Statistics:
-
Statistical Measures: Many statistical measures, such as percentages, proportions and rates, rely on percentage calculations. Understanding percentages is essential for interpreting and analyzing data effectively.
-
Surveys and Polling: Survey results are often presented as percentages to illustrate the proportion of respondents who chose a particular option.
4. Everyday Life:
-
Tipping: Calculating tips in restaurants often involves determining a certain percentage of the bill amount.
-
Recipe Scaling: Adjusting recipe quantities requires understanding proportions and percentage calculations.
-
Sales and Promotions: Understanding discounts and percentage offers helps in making informed purchasing decisions.
Beyond the Basics: Understanding Percentage Increase and Decrease
Beyond calculating a simple percentage, understanding percentage increase and decrease is equally important:
Percentage Increase:
This calculates the proportional change when a quantity increases. The formula is:
Percentage Increase = [(New Value - Original Value) / Original Value] * 100
For instance, if a stock price increases from $100 to $120, the percentage increase is:
[(120 - 100) / 100] * 100 = 20%
Percentage Decrease:
This calculates the proportional change when a quantity decreases. The formula is:
Percentage Decrease = [(Original Value - New Value) / Original Value] * 100
If the stock price drops from $120 to $95, the percentage decrease is:
[(120 - 95) / 120] * 100 = 20.83%
Error Analysis and Precision
In percentage calculations, precision is crucial. Rounding errors can accumulate, especially in complex calculations involving multiple percentage changes. It's essential to maintain a sufficient level of precision throughout the calculation and only round the final result to the desired number of decimal places. Using a calculator or spreadsheet software can minimize the risk of errors and ensure accuracy.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a valuable skill with numerous applications. This comprehensive guide demonstrates how to calculate 95 out of 120 as a percentage, highlighting various calculation methods and practical applications. By understanding these concepts, you can effectively analyze data, make informed decisions, and communicate numerical information clearly and concisely. Remember to consider the context, maintain precision, and choose the appropriate method for your specific needs. Mastering percentage calculations empowers you to navigate various aspects of life with greater confidence and efficiency.
Latest Posts
Latest Posts
-
How To Find Center Of Sphere
May 12, 2025
-
How Do You Calculate The Curvature Of The Earth
May 12, 2025
-
Cuanto Es 400 Gramos En Libras
May 12, 2025
-
Greatest Common Factor Of 25 And 100
May 12, 2025
-
What Day Was It Six Months Ago
May 12, 2025
Related Post
Thank you for visiting our website which covers about 95 Out Of 120 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.