Are 3/4 And 9/12 Equivalent Fractions
Treneri
May 12, 2025 · 5 min read
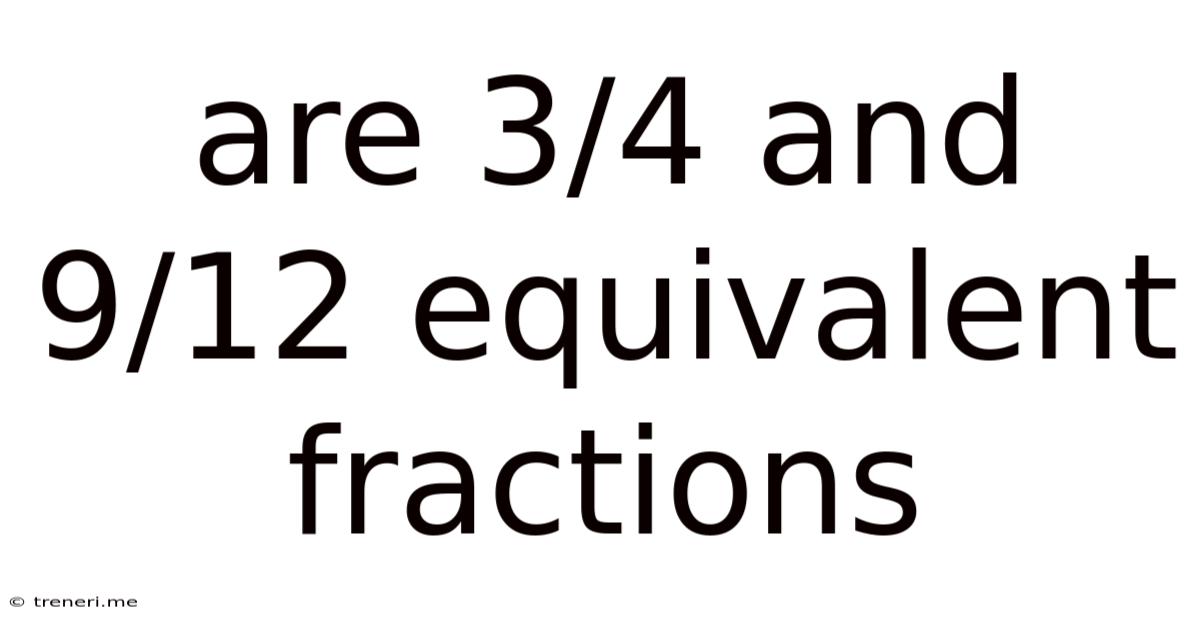
Table of Contents
Are 3/4 and 9/12 Equivalent Fractions? A Deep Dive into Fraction Equivalence
Understanding equivalent fractions is fundamental to mastering mathematics. This comprehensive guide will explore whether 3/4 and 9/12 are equivalent fractions, delving into the concept of fraction equivalence, providing multiple methods for verification, and exploring real-world applications. We'll also touch upon the importance of simplifying fractions and how it relates to equivalent fractions.
What are Equivalent Fractions?
Equivalent fractions represent the same proportion or part of a whole, even though they are written with different numerators and denominators. Think of it like slicing a pizza: you can have one-half (1/2) of a pizza, or you can have two-quarters (2/4), or four-eighths (4/8) – they all represent the same amount of pizza. These fractions (1/2, 2/4, 4/8) are equivalent fractions.
The key to understanding equivalent fractions lies in the relationship between the numerator and the denominator. Equivalent fractions are created by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process maintains the ratio between the numerator and denominator, ensuring the fraction represents the same value.
Methods to Determine if 3/4 and 9/12 are Equivalent
Let's explore several ways to determine if 3/4 and 9/12 are indeed equivalent fractions:
1. Simplifying Fractions
Simplifying a fraction involves reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
- Simplifying 9/12: The GCD of 9 and 12 is 3. Dividing both the numerator and denominator by 3, we get: 9 ÷ 3 = 3 and 12 ÷ 3 = 4. Therefore, 9/12 simplifies to 3/4.
Since 9/12 simplifies to 3/4, this confirms that 3/4 and 9/12 are equivalent fractions.
2. Cross-Multiplication
Cross-multiplication is a powerful technique to check the equivalence of two fractions. We multiply the numerator of the first fraction by the denominator of the second fraction and vice-versa. If the products are equal, the fractions are equivalent.
- Cross-multiplying 3/4 and 9/12:
- 3 * 12 = 36
- 4 * 9 = 36
Since both products are equal (36 = 36), this confirms that 3/4 and 9/12 are equivalent fractions.
3. Visual Representation
Visual aids, such as diagrams or pie charts, can effectively demonstrate the equivalence of fractions. Imagine two identical circles.
- Divide the first circle into four equal parts and shade three. This represents 3/4.
- Divide the second circle into twelve equal parts and shade nine. This represents 9/12.
Visually comparing the shaded areas of both circles clearly shows that they represent the same proportion of the whole, confirming that 3/4 and 9/12 are equivalent fractions.
4. Finding a Common Denominator
Another method involves finding a common denominator for both fractions and then comparing the numerators. A common denominator is a multiple of both denominators. In this case, a common denominator for 4 and 12 is 12.
- Converting 3/4 to an equivalent fraction with a denominator of 12: We multiply both the numerator and the denominator by 3 (because 12 ÷ 4 = 3): (3 * 3) / (4 * 3) = 9/12.
Since both fractions now have the same denominator (12) and the same numerator (9), this proves that 3/4 and 9/12 are equivalent fractions.
The Importance of Simplifying Fractions
Simplifying fractions, also known as reducing fractions to their lowest terms, is crucial for several reasons:
- Clarity and Understanding: Simplified fractions are easier to understand and interpret. For example, 3/4 is easier to grasp than 9/12 or 15/20.
- Easier Calculations: Calculations involving simplified fractions are simpler and less prone to errors. Working with 3/4 is significantly easier than working with 9/12, especially in more complex calculations.
- Standard Form: Simplifying fractions ensures that fractions are presented in their standard form, improving communication and consistency in mathematical work.
- Identifying Equivalence: As demonstrated, simplifying fractions is a key method for identifying whether two or more fractions are equivalent.
Real-World Applications of Equivalent Fractions
The concept of equivalent fractions finds applications in various real-world scenarios:
- Baking and Cooking: Recipes often require fractions of ingredients. Understanding equivalent fractions allows for adjustments in recipe sizes without altering the proportions. For example, if a recipe calls for 3/4 cup of flour, you can easily substitute 9/12 cup.
- Construction and Engineering: Equivalent fractions are essential in precise measurements and scaling drawings in architecture, engineering, and construction projects.
- Finance and Business: Working with proportions and percentages in financial calculations and business analyses involves a deep understanding of fractions and their equivalence.
- Data Analysis: Equivalent fractions are useful when dealing with proportions and ratios in statistical analysis and data visualization.
Beyond 3/4 and 9/12: Exploring Other Equivalent Fractions
While we've focused on 3/4 and 9/12, the principles discussed apply to any pair of fractions. To find equivalent fractions, simply multiply or divide both the numerator and the denominator by the same non-zero number. For example, other equivalent fractions to 3/4 include:
- 6/8 (multiply by 2)
- 12/16 (multiply by 4)
- 15/20 (multiply by 5)
- 21/28 (multiply by 7) and so on.
Conversely, you can find equivalent fractions by dividing the numerator and denominator by their greatest common divisor.
Conclusion: The Equivalence of 3/4 and 9/12
Through multiple methods – simplification, cross-multiplication, visual representation, and finding a common denominator – we have conclusively demonstrated that 3/4 and 9/12 are indeed equivalent fractions. Understanding equivalent fractions is essential for mathematical proficiency and its applications across numerous real-world fields. Mastering this concept will undoubtedly enhance your problem-solving abilities and improve your overall mathematical comprehension. Remember to practice regularly and explore different methods to solidify your understanding. The ability to quickly and accurately identify and work with equivalent fractions is a valuable skill that will benefit you throughout your mathematical journey.
Latest Posts
Latest Posts
-
How Many Ounces In 31 Grams
May 14, 2025
-
How Many Days Is 640 Hours
May 14, 2025
-
How Many Calories Do I Burn Pumping
May 14, 2025
-
10 Ml Is The Same As
May 14, 2025
-
How Many Cups In 96 Oz
May 14, 2025
Related Post
Thank you for visiting our website which covers about Are 3/4 And 9/12 Equivalent Fractions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.